

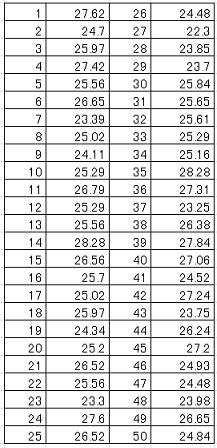
1.検証データ
ある製品の特性検査工程での不良率が少し高いため、製造責任者から製品開発担当者に調査依頼の要請があり、開発担当者は製造在庫品から50個出庫し特性を測定した。その結果は以下の通りであるが、この製造プロセスの工程能力を評価せよ。なおこの特性値の検査規格は両側規格でTc=25、USL=30、LSL=20である。
2.点推定の評価
以下表に点推定値における試料統計量と工程能力及びヒストグラムを示す。
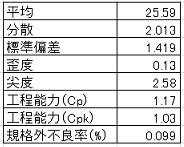
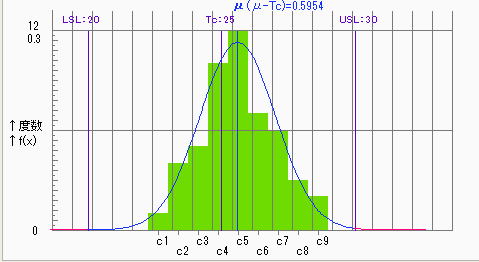
平均値は規格中心値より上側に位置しているがCpkのダウン率は0.12(K=0.88)と、あまり大きな外れではない。不良率は0.1%程度と予測される。
2.仮説検定による評価
2.1分散の検定
仮説検定ではCpk(正確さ+精度)を同時に検定することはできないので、正確さと精度は別々に検定することになる。Cp(精度)の検定は「分散がある値より小さい」事を問う行為となり、仮説の設定は以下のようになり、σの具体的な値は以下のように決定できる。
規格幅:(USL-LSL )=10
仮想母集団:N(μ,σ)=(25,10/8)
帰無仮説 H0:σ2=1.5625 対立仮説 H1:σ2<1.5625(片側検定)
一般的な基準として工程能力(Cp)は1.3を言われているので、規格幅(USL-LSL=10)に対し8σであるかがその判断になり、母集団の分散σ2≦(10/8)2=1.5625が一応の指標となる。この仮説検定においてH0が棄却されれば工程能力Cp≧1.3を積極的に支持できることになるが、試料統計量から求められる工程能力Cp≒1.17<1.3と下回っているため、この仮説検定は最初から棄却されないことは明らかである。SA&RA
ProXの検定結果を以下に示す。
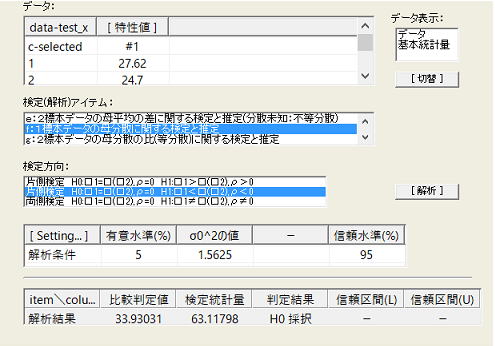
当然棄却されずこのプロセスの工程能力Cp≧1.3は否定された。検定では採択された条件は積極的には支持できないので、勿論Cp=1.3であるかもこの段階では曖昧で疑わしい。次の判断基準としてCp≧1.0(σ2=(10/6)2=1.6672)を以下の仮説で検定してみよう。今回は仮説H1の設定が試料統計量(σs=1.419)を上回っているため、実施する以前に棄却されるかされないかの判断はできない。
帰無仮説 H0:σ2=2.778 対立仮説 H1:σ2<2.778(片側検定)
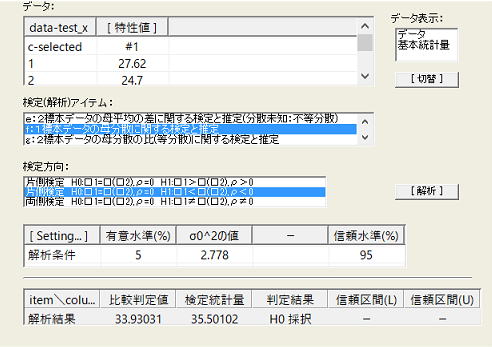
比較判定値に対し検定統計量がかなり近い値になったが、同様に棄却されなかったので工程能力は1.0以上ともいえず、また1.0であるかも積極的には支持できない。仮説検定では棄却限界を求める行為は常套手段ではないが、σの値を段々と大きくしていけばある値で棄却される筈である。実際にやってみると以下の仮説検定値で棄却された。
帰無仮説 H0:σ2=2.95 対立仮説 H1:σ2<2.95(片側検定)
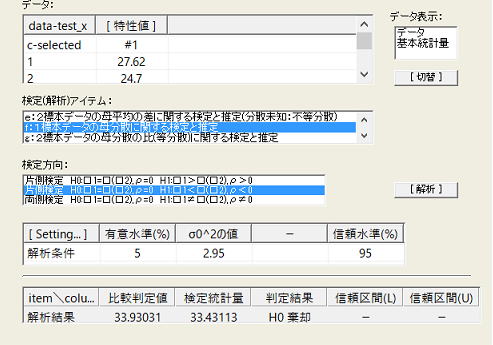
この場合の工程能力は10/(1.718×6)=10/10.308≒0.97で、棄却されたのでこの工程能力指数は積極的に支持できる。点推定値(1.17)より低く見積もられているが、これはn数が検定統計量に反映された結果、母集団の分散が点推定値(2.013)より大きく見積もられたことによる。このように分散の検定は、工程能力指数のCpを検定していると思えばよい。
2.2平均の検定
この場合は正確さ、つまり母平均がある値より大きいか小さいかを問う行為と言えるが、分散の検定がCp(精度)の検定に対してCpk(“正確さ”+精度)の検定と考えればよい。Cp→Cpkに変換する際のダウン率と考えれば更に分かりやすく、Cpk=(1-K)Cpより「Kの値がある値より小さい」事を問う仮説となる。分散の検定結果からCp→Cpkのダウン率は大きな値は許容できないためK<0.1(Cpの0.9以上)を問うことにすると、今回の試料平均は規格値(Tc=25)を僅かではあるが上回っており、K=|(
Tc-μ0)|/(USL-LSL)/2より仮説の設定は以下のようになる。 この仮説検定においてH0が棄却されれば、Cpk≧Cp×0.9を積極的に支持できることになる。
帰無仮説 H0:μ=25.5 対立仮説 H1:μ<25.5(片側検定)
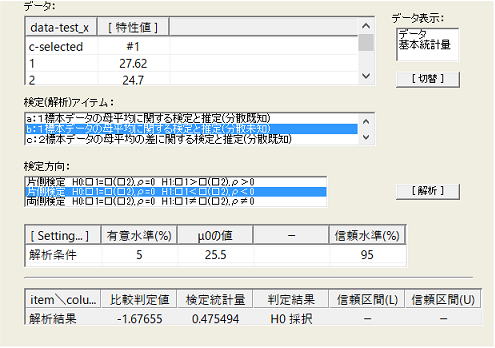
棄却されずK≦0.1以下とはいえないことから、CpkはCpの0.9以下まで低下が見込まれることになる。棄却限界を探ると26.0(K≦0.2)で棄却された。
帰無仮説 H0:μ=26.0 対立仮説 H1:μ<26.0(片側検定)
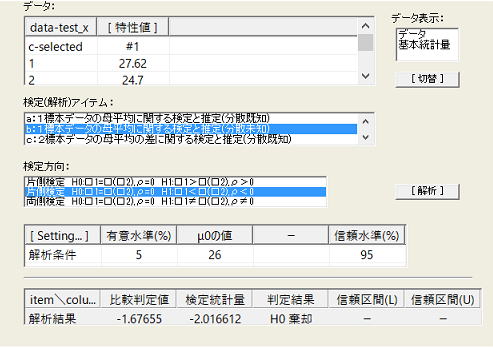
これよりK<0.2は積極的に支持できることになり、Cpkは少なくともCpの0.8以上はあると判断できる。以上のことから仮説検定による評価ではCpkは0.97×0.8(≒0.78)程度と推定され、工程能力はやや不足との判断になる。但し何れの検定も有意水準
5%の結果でありやや厳しい評価となる。
3.母集団の推定による評価
3.1母平均で評価
試料統計量Ns(μs,σs)から母集団N0(μ0,σ0)を推定する際に、分散(標準偏差)は点推定値のまま平均のみ一定の信頼水準(例:95%)で区間推定し、N0(25.59-δμ~25.59+δμ, 1.419)として評価することになる。理想は95%信頼区間の最悪条件で工程能力Cpk≧1.0~(信頼区間での評価であり1.0までを許容する)であるが、信頼区間は信頼水準の値と試料数によって大きく変化する。評価する際の信頼水準は高くしたいところではあるが、少ない試料数で信頼水準を上げると信頼区間が広くなり評価者には厳しい判定となる。しかし実情は多くの試料数を得ることは困難な場合が多く、高い信頼水準(90%~)に厳格に拘る必要性はない。つまり95%信頼区間で工程能力Cpk≧1.0を満足しない場合は、信頼水準を徐々に下げ80%までにCpk≧1.0を満足すれば、そのプロセスはOKと判断しようというものである。
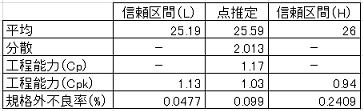
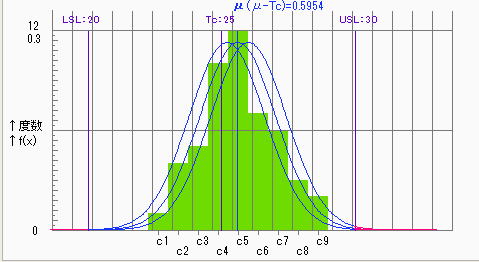
●95%信頼区間における評価
●80%信頼区間における評価
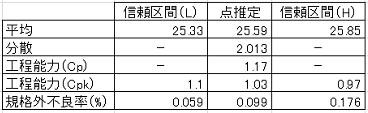
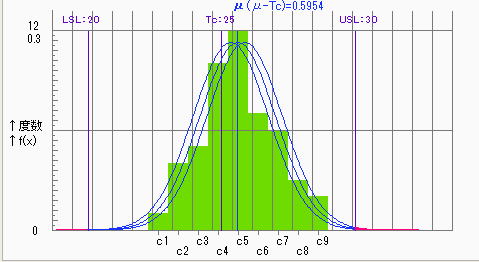
信頼水準を95%から80%に下げることによりCpkの推定値は上がってはいるが、80%信頼区間でもCpk=0.97であり1.0を下回っており満足しているとは言えないとの結果である。
3.2母分散で評価
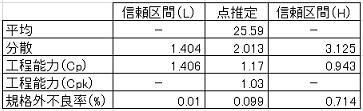
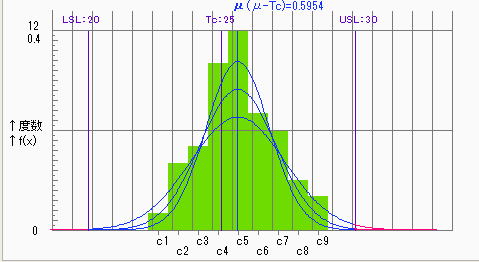
標本サンプルデータの点推定値Ns(μs,σs)から母集団N0(μ0,σ0)を推定する際に、平均は点推定値のまま分散のみ一定の信頼水準(例:95%)で区間推定し、N0(25.59,1.419-δσ~1.419+δσ)として評価することになる。統計理論からは分散変動の方がより厳しい評価となる。
●95%信頼区間における評価
●80%信頼区間における評価
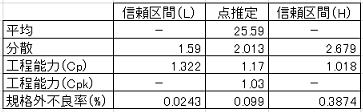
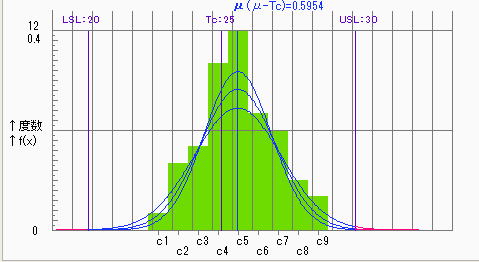
95%信頼区間におけるCp=0.912とやや不足であるが、80%信頼区間ではCp≧1.0を満足している。
3.3母平均と母分散で評価
標本サンプルデータの点推定値 N s(μs,σs)から母集団N 0(μ0,σ0)を推定する際に, 平均と分散の両方を一定の信頼水準(例:95%)で区間推定し, N 0(10.006-δμ~10.006+ δμ, 0.0064-δσ~0.0064+δσ)として評価することになる。 なおこの場合は各信頼区間の分散の最悪条件(すなわち区間幅の最大値)、すなわちCp=1.17に対して平均の区間幅内でCpkがどれ程ダウンするかを評価していることになり、評価者にとっては最も厳しい評価となる。
●95%信頼区間における評価
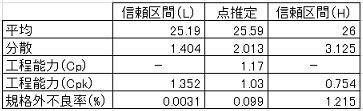
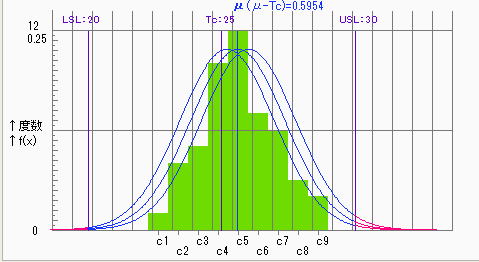
●80%信頼区間における評価
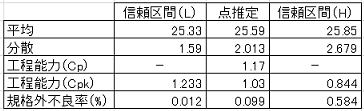
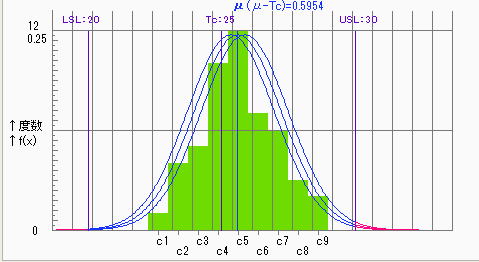
信頼水準順を80%に低下させてもCpk=0.84となっており、工程能力がやや不足との評価となった。
4.評価の纏め
4.1仮説検定
仮説検定では有意水準(α)は一般的に5%に設定(推定の信頼水準では95%に相当)されるので、エンジニアが開発プロセスで検証する試料数(3,5~10~20個程度)では、殆どの場合厳しい評価となる。仮説検定の精度と正確さの両方を考慮した工程能力指数は、点推定値のCpk=1.17に対して0.78とかなり低く見積もられている。仮説検定では母集団の分布をイメージしにくいが、工程能力(Cp及びCpk)を評価する意識で仮説を設定することが重要である。今回の演習は製造プロセスの評価であるが、設計検証における機能特性の評価も全く同様に評価できる。
4.2母集団の推定
仮説検定の場合判断決定の二つの誤り(リスク)の兼ね合いもあり、有意水準(α)を大きく変更して検定することには躊躇があるが、推定の信頼水準については評価者の任意性が高い。信頼水準は単純には実験の確かさ(95%とは同じ検証を20回実施すると1回は誤った判断を下す)なので、信頼水準を少し低く設定することで開発プロセスにおける試料数の少なさの影響を低減できる。管理人の経験からは信頼水準は80%程度まで下げても評価を誤る可能性は殆どなく、むしろ試料数が少ないことから不合格と判断する方が余程影響は大きい。今回の例では80%信頼区間のCpk=0.84なのでやや不足との判断は止むを得ないが、仮説検定より圧倒的に母集団をイメージしやすい事もあり、管理人は推定を用いて母集団を評価する事が多かった。