1.概念
仮説検定と推定は方法は異なるものの、いずれも母集団のパラメータに関心が及ぶことは同じである。推定の考え方はある意味柔軟性があり仮説検定より母集団をイメージしやすく、製品の特性値など一つの母集団を対象とする場合は、管理人は検定より推定を用いて検証する事が多かった。前者が観察されたデータが特定の母集団から抜き取られたものと判断していいかを問うのに対し、推定は以下のような考え方に基づく。同じ母集団から何回かサンプリングした場合、その試料統計量(平均、分散)は概ね母集団のパラメータに近い値を取ることは容易に想像できる。平均を例に考えると試料平均値は母平均付近になる確率は高く、母平均から離れた値を取る確率は低くなる。このことは逆の見方をした場合、試料平均値が得られた結果の理由として、”試料平均値付近”に高い確率で母平均がある(だろう)とする考え方が成り立つ。この”試料平均値付近”を別な言葉で表すと「試料平均値を中心としたある範囲」となり、統計理論によりこれを定量化(数値化)する行為が区間推定の概念である。平易には試料統計量から母集団のパラメータを言い当てる行為であるが、ランダムサンプリングによるたかだか1回の観察データが、評価者にとって運の良いデータか悪いデータかまでの判断には及ばない。
2.信頼区間と信頼係数
区間推定は「~の付近にあるだろう」といった具合に、母集団のパラメータを一定の範囲で考えようというものである。「信頼区間」は母集団のパラメータが含まれる範囲、「信頼係数」は信頼区間の範囲内に母集団のパラメータが含まれる確率である。信頼区間は直観的に分かるが信頼係数はどのように考えればいいだろうか。これは言い当てる確率と考えれば分かりやすく、信頼係数が大きいとは言い当てる確率が高いことである。評価者が製品の機能特性が仕様範囲を満足しているかを検証(推定を用いて)する際、言い当てる確率は出来るだけ高く(信頼係数を大きく)したいところであるが、信頼区間と信頼係数は密接な関係があり信頼係数を大きくすると信頼区間は広くなる性質を持つ。これは逆に考えると分かりやすく、関心がある事象について幅を広くして問い掛けた方が、言い当てる確率が高くなるのは容易に理解できよう。区間幅が狭い場合と広い場合の何れが評価者にとって都合が良いかは、狭い方が仕様範囲に入りやすいのは明らかである。結局エンジニアは当てようとする確率(信頼係数)と信頼区間幅の狭間で苦労することになるが、この天秤を左右するパラメータは結局試料数であり、仮設検定同様にサンプルサイズが大きな鍵を握っていることになる。
3.点推定とは
我々は知りたい情報(設計品質、工程品質などのプロセスの安定性)を得たいとき、多くの場合その全てを調べることはできないためサンプリングという手段を用いる。このとき知りたい情報の対象である集団を母集団、抜き出したものを試料(あるいはサンプル)という。従って我々が知り得る情報は、母集団そのものではないことは明白である。知りたい情報の代表的な例を以下に示す。
1) “母”平均は規格中心値に近い値か。
2) “母”標準偏差(ばらつき)は規格範囲内か。
これをイメージ化すると以下のように表せる。

本来は上の式のように母集団のパラメータで判断しなければならないが、評価者が知り得る情報は試料統計量のみなので左辺(母集団のパラメータ)は何れも未知のため、このままでは結論は得られない。統計的な考えが及ばない場合は往々にして“次の一手”が登場する。
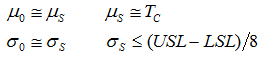
しかし試料統計量を母集団のそれと置くこの論理展開には大きな落とし穴がある。それはサンプルサイズが全く反映されていない点で、サンプルサイズが非常に大きければ成り立ちそうであるが、逆に非常に小さい(1~2個)場合は明らかに無理(情報量が不足)であることに気付く。上記のように試料統計量をそのまま母集団のパラメータとする行為を「点推定」という。点推定は区間推定の特別な場合で、パラメータが含まれる範囲は極小(区間幅がゼロ)で信頼係数は極限まで小さい(ゼロ)。言い当てる確率はゼロなので、勿論検証結果としてこれを言い張ることはできない。サンプリングという手段を用いる以上我々は“この問題”を避けて通れないが、統計的な考え方を導入することで“この問題”を解決できる。言い換えればサンプリングという情報収集手段では、統計的な考え方は外せないことになる。
4.区間推定の考え方
仮説検定の理論編においても述べたが、母集団から抜き取られたランダムサンプリングの試料統計量(平均、分散)は、以下のような分布になることが知られている。例として母平均の区間推定を考えよう。試料平均値は母平均μ0を中心に分布しており、1回のサンプリングにおいては確率の範囲内でどんな値も取り得るが、前述したように母平均μ0付近になる確率は高くなる。ここで”柔軟的な考え方”として、「仮説検定における棄却域(~のような低い確率領域)からは試料平均は出ない」と、割り切って考えようというものである。この考え方から区間推定における信頼区間と信頼係数は、以下の様に定義される。
信頼区間:仮説検定の採択域
信頼水準:有意水準から(1- α)%
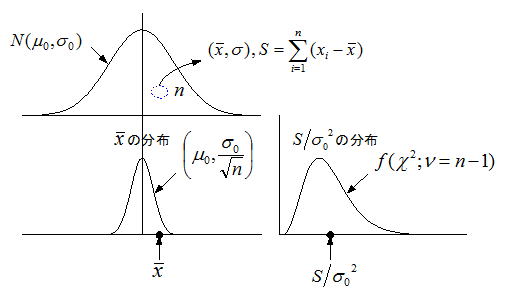
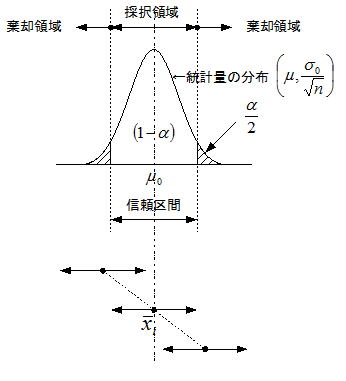
つまり母平均は、信頼区間内に信頼係数(1-α)%の確率で存在するとの論法になる。但し区間推定は試料統計量が得られた結果の後天的な理由付けであり、それが評価者にとって運の良いデータか悪いデータかまでは関心が及ばず、試料統計量の値(区間幅の中心値:点推定値)により上右図のように変化する。従って試料統計量が仮に棄却領域に位置したら、図のようにその区間内にμ0はない。つまり何回かのサンプリングにおいてα=5%であれば、20回に1回程度は信頼区間内に真の母平均μ0が含まれないリスクがあることを意味する。
5.母集団の捉え方
仮説検定では個々の母数(平均又は分散)のみに着目するため、それ自体の真偽は問えるが母集団全体の分布はイメージしにくい。対して推定は母集団を分布の位置と形として捉えられるためプロセスの全体像が掴みやすく、更に最悪条件においてどの程度の確率で規格外が発生するかも推定可能である。勿論その推定確度(信頼係数をどこまで上げられるか)は、仮説検定同様に試料数が大きく関係することは変わらない。
ある母集団の試料データ(μs,σs)から、母集団を推定するイメージを下図に示す。試料データをそのまま用いた(点推定の)分布、μ又はσの信頼区間の片側みを考慮した分布、μとσの両方の信頼区間を考慮した分布である。試料統計量から規格範囲(USL-LSL)との整合性を検証する場合は、正確さ(μ)と精度(σ)はこの範囲まで大きく見積もる必要性があることを示している。なおこれらの情報はツールを使用することで容易に得られるが、管理人の経験としてプロセスの変動要素は、正確さが主体のものと精度が主体のものとに分けられ、全てのプロセスでμとσの両方の信頼区間を考慮する必要性は必ずしもないように思われる。仮に正確さも精度も変動するようなプロセスがあったとするなら、そのプロセスは不必要な検査工程をいくつか設けなければならない可能性が高く、本来なら製造移管してはならないプロセスである。なお何れか判断がつかない全く新しいプロセスを検討する場合は、最悪条件(両方)で検証する必要がある。
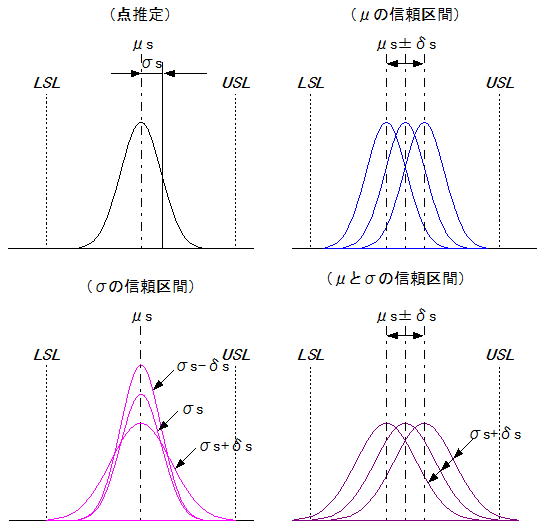
仮説検定の有意水準(α=5%)は値を変更して検定することにはかなり躊躇があるが、区間推定の信頼係数は80%~95%を採用しても大きな違和感は覚えず、この辺りが区間推定の柔軟さといえるだろう。信頼係数は90%以上が推奨されるがエンジニアが扱う試料数は限られるため、90%以上確保した上で整合性のOK(例えば工程能力指数Cpk≧1.0)を得ようとすると、特に分散を推定する際の影響が大きくかなり厳しい状況になる。何れにしても我々エンジニアが扱う試料数(試作段階レベルの試料数は概ね5~20個程度であろう)では、母集団のばらつきを正確に推定することは、仮説検定も推定も元々困難であるとの意識が必要である。ばらつきをある程度正確に見る観点では、自由度(データ数)がある程度大きくなるDOE(実験計画法)の方が情報確度は高い。DOEにおける誤差分散(Ve)は母分散(σ2)の推定量となり母標準偏差を導く値になるため、実験で扱った特性(Y)のばらつきを検討する際の重要な情報となる。
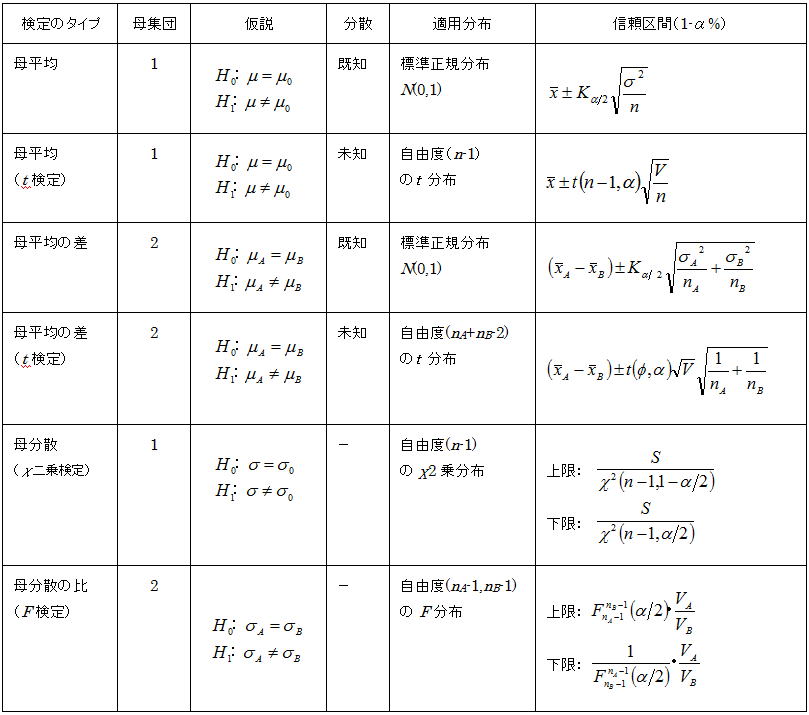
6.適用分布と推定方法
以下の表に推定するパラメータにより適用される統計量の分布と、信頼限界を求める式を示す。仮説検定における検定統計量同様に、我々エンジニアはこれらの情報を細かく知っておく必要はなく、情報処理はツールに任せて結果をどう捉えるかだけに注力すればいいい。