１．概念
仮説検定はこの分野の多くの文献で相当数の頁が割り当てられ、それはシックスシグマなどの実践文書でも同様である。仮説検定の理論自体はそれ程難しいものではないが、製品の機能特性が仕様を満足しているかを平均と分散（標準偏差）で仮説検定しても、我々が最も知りたい母集団のイメージまでは掴みにくい点がある。これは検定結果として仮にH0が棄却（この結果の捉え方は後で述べる）されたとしても、この結果から設計（若しくは製造プロセス）をどのように補正しなければならないかまでは、正直分からない（アクションが立てにくい）ことが多い。もう一つの理由として、仮説検定は平易には「観察されたデータが特定の母集団から抜き取られたものと判断していいか？」の確率問題（その確率は大きいか小さいか？）といえるが、大きいか小さいかを判断するために必要な試料数が、エンジニアが開発ステップで扱う試料数（3,4,5～15個程度）と元々折り合わず、この観点からは開発ステップにおける検証ツールとしてはやや不向きで、どちらかと言えば製造プロセスでの検証に向いているといえる。
このように書くと統計分野の諸先生から何か云われそうだが、実際に実践した上での経験による判断なので仕方がない。「ではまるで役に立たないか」と言えばそうではなく、仮説の立て方さえ習得すれば面倒な計算はツールに任せることができるので、客観的な評価を得るための有効なツールである事には違いない。エンジニアが仮説検定を実践するには越えなければならない二つのハードルがあり、一つはエンジニアが最も知りたい情報（例えばその機能特性は仕様を満足しているか）についてどの様に仮説を立てればいいか、もう一つは裁判に例えた場合の有罪（H0棄却）と無罪（H0採択）の判決結果について、その信憑性が大きく異なる点の理解であろう。一般的な裁判では「無罪判決」なら被告は喜ぶべき結果となるが、仮説検定における無罪は評価者にとっては必ずしも喜べないという点がある。実際管理人もこの全てを理解するまでに少し時間を要した経験がある。
さて話を戻して我々が最も知りたい情報は、設計品質、工程品質など特定の母集団の品質状況であり、より具体的な例を示すなら以下のような問い掛けになる。
1) “母”平均は規格中心値に近い値であるか。
2) “母”分散（ばらつき）は規格範囲内に収まるか。
この判断を得るには母集団のパラメータ（μ0,σ0）が知られていなければならないが、エンジニアが試作品で知り得る情報はあくまで試料統計量であり、何らかの方法で母集団の情報に置き換える必要がある。仮説検定はこの情報を置き換えた上で確率の判断を決定してくれるツールであるが、確率を計算するための密度関数の母数にサンプルサイズが取り込まれるため、評価者の意に関係なくサンプルサイズの影響を受けることになる。
２．仮説とは
仮説検定をする上で評価者がやらなければならない最も重要な手順の一つが仮説の設定である。例えば「成人男子の平均身長は167cm」と想定はできるが、これが“本当にそうであるか”
は定かではない。このように母集団のパラメータについて想定値を特定（ μ=167cm）することを”統計的仮説”というが、仮説を設定する（立てる）際は母集団のパラメータが”そうである（正しい）”と肯定する側と、”そうでない（正しくない）”と否定する側の二つの仮説を並立する。これを裁判に例えるなら、予め無罪（正しい）と有罪（正しくない）の判決文を用意しておくことになる。仮説検定では得られた情報（試料統計量）から、裁判では検察が提出した証拠などに基づきこの何れかを採択することになるが、この時前者を帰無仮説（H0 ）後者を対立仮説（H1）という。表面的には帰無仮説の方が重要と思われるかもしれないが、仮説の主役は対立仮設であり帰無仮説はあくまで脇役（対立仮説が決まれば、それを自動的に肯定する内容として決まる）である。
３．仮説検定の考え方
3.1 試料統計量と母集団の情報
仮説検定は前述したように、試料統計量（μs,σs）がどのくらいの確率で得られるかの確率問題である。非常に分かり易い例として偏差値が挙げられるが、偏差値は（μ,σ）=（50,10）の正規分布と定義されており、偏差値70点の発生確率は上側2σの%点（u =2.0）の確率（下側：97.72%,上側：2.28%）として容易に求められる。偏差値のように試料統計量の振舞い（どのような分布に依存するか）が分かっていれば、サンプルデータから推定される試料統計量の%点から発生確率を容易に求めることができる。試料統計量はどのような情報を持ち、どのように振舞うかを考えてみよう。N0 ( μ0 ,σ0 ) の母集団を考え、n 個の試料による抜き取り検査を仮に100回試行したとすると、試料統計量（平均、変動（偏差平方和））は下図のような分布になることが知られている。各分布には母集団の母数 ( μ0 ,σ0 )の情報が反映されており、更に分布を決定するパラメータとして試料数（n）が何れにも入っている点が重要である。試料統計量の分布は、母集団の母数と試料数でその振る舞いが決定することが分かる。これらの分布を用いることで試料統計量が得られる確率を知ることはできるが、我々がそれを知り得る機会はたかだか1～2回であり、母集団の情報が十分取り込まれているか（サンプリングの偏りがないこと）が重要である。
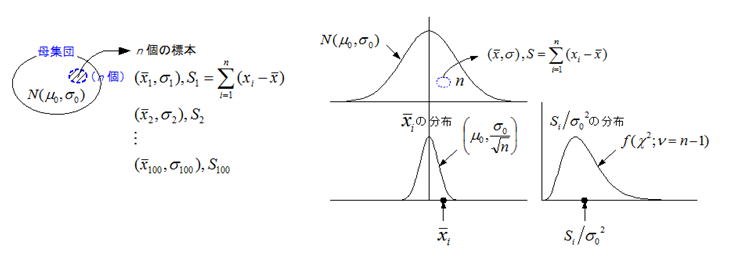
上の分布の内平均値の分布は分散が既知の場合の平均値の検定、自由度(n -1)のχ二乗分布は母分散の検定に適用される。この他自由度(n -1)のt 分布は分散が未知の場合の平均値の検定、自由度(n1-1),(n2-1)のF分布は分散比の検定に適用される。
3.2 確率の判断基準
3.1項の各分布を用いて試料統計量の発生確率（上側若しくは下側）が分かったなら、次の手順としてその確率が大きいか小さいかを判断することになる。ここではその基準をどのように考えればいいかについて、例として加工寸法がある目標値(Tc)であるかを仮説検定する場合を考えよう。前述したように対立仮説が主役であり、否定する側の仮説となるのでμ≠Tcを先に立てることになり、帰無仮説はそれを自動的に肯定することになるのでμ＝Tcとなる。
帰無仮説：μ＝Tc
対立仮説：μ≠Tc
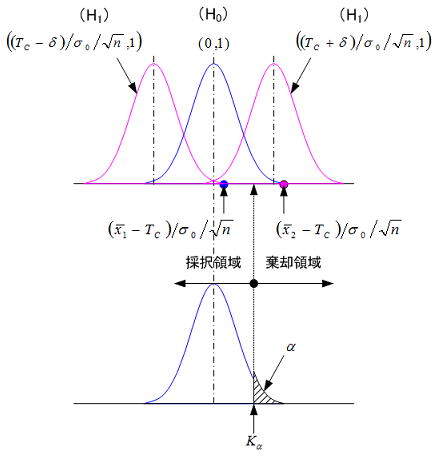
分り易くするために母集団（母平均）が目標値と一致している場合、目標値から±δ（任意の値であり大きさは拘らない）離れた位置に分布した場合を想定する。当然それらの母集団から得られる試料統計量（ここでは平均値）の分布も、それに応じて下図のように位置（x軸は標準化軸として示してある）が変化する。分布の位置を仮説の観点で言い換えると、目標値と一致とはH0が正しいときの分布位置、±δ離れた位置とはH0が正しくないときの分布位置になり、各H1の分布の位置(Tc±δ)/(σ0/
)は、H0における位置(0)からの距離を%点で示したものである。以上の想定において、偶々得られた二つの統計量（x1,x2）について考えてみよう。なお厳密には母分散が既知の場合と未知の場合では適用する試料統計量の分布は異なるが、ここでは考え方の説明が目的であり前者に限定して考えるものとしよう。分布の位置と統計量の位置から、H0が正しいときの分布に対してはx1が得られる確率は大きく、x2が得られる確率は小さい。一方H0が正しくない（H1が正しい）分布に対しては、逆にx2が得られる確率は大きくx1が得られる確率は小さい。これらの関係は以下のような合理的な考え方に、繋げることができる。
x1 ：H0が正しいときの分布から得られた
x2 ：H0が正しくない（H1が正しい）ときの分布から得られた
つまり試料統計量（平均値）としてx1が得られたら、H0の分布から得られた確率が高いので「H0は正しい」、逆にx2のようにH0の分布から得られた確率が低い（言い換えるとH1の分布から得られた確率は高い）場合は、「H0は正しくない」と判断しようというものである。これが仮説検定が確率問題であるとの所以である。この高い低いを判断する基準（確率）を有意水準（α）といい、一般的な値としてα＝5%が採用される。電卓しかなかった時代では、以下のように得られた試料統計量と有意水準の%点の値を比較していたが、今やPC上で正規確率は瞬間的に計算できるため、試料平均が得られる確率と有意水準を直接比較しても結果は同じである。
試料平均の%点（xi＞Tc）：
判断基準の%点：Kα=5%=1.96
どのような統計的判断も、データに基づいて可能な限り正しい（客観的）判断を決定しようとの試みがあるが、統計理論に基づいた判断といえども100%
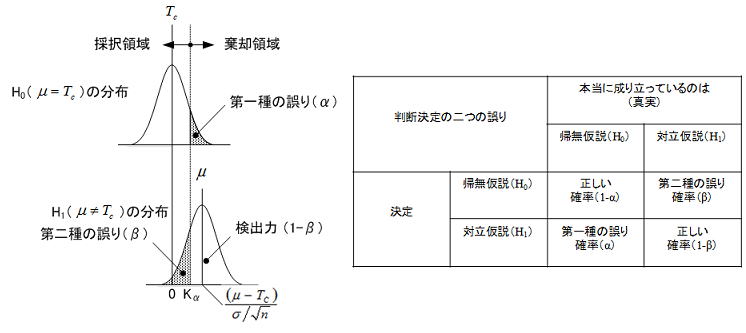
言い切ることはできず、仮説検定においても以下の二つの誤り（リスク）が存在する。特に第二種の誤りについては、H0が正しくない分布の位置（目標値からのズレの度合い：3.1項のδの大きさ）とサンプルサイズにより大きく変化するため、評価者がリスクの大きさを直観的に捉えにくく、これが仮説検定の分かりにくさの一つの要因といえる。下図に平均を検定（目標値Tcとの差）する際のこれらの関係を示すが、μ≠Tcの位置はあくまで一例であり実際にはいろいろな位置を取り得る。
1) 第一種の誤り
本当は帰無仮説が正しい（H0の分布）のに H0を棄却する誤りで、「良品なのに不良品と判定して出荷しない」誤りになる。H0が正しい場合でもサンプリングの偏りなどで、3.2項におけるx1が有意水準α%の棄却領域に入る確率は小さいながら常にある。これを第一種の誤りといい仮説検定の理論上の仕組みからこの確率は常に一定で、検定の有意水準であることからαで表す。
2) 第二種の誤り
本当は帰無仮説が正しくない（H1の分布）のにH0を棄却しない誤りをいい、「不良品なのに良品と判定して出荷する」誤りになるため第一種の誤りより影響は大きい。これはH0が正しくない場合でも、試料統計量が採択領域に入る確率が高くなる場合（μ-Tcの差が小さい、又は分布のばらつきが大きい）があり、これを第二種の誤りといいその確率をβで表す。H1の分布の位置関係から、H0が正しくない位置の式
よりTcからのズレ具合とサンプルサイズにより大きく変化することが分かる。H0が採択された場合はβが十分小さい（言い換えると検出力(1-β)が十分大きい）ことを検証する必要がある。これらの関係を纏めた表を下に示す。
評価者はこれらのリスクをどのように捉えればいいだろうか。リスクは誤った判断を下す確率と捉えれられるので例えばH0が棄却との結果が得られた場合、同じ検証を20回実施すると1回程度は誤った判断（H0が正しいのに棄却する）を下す可能性があることになる。仮説検定では二つのリスクは以下のように振る舞うが、特にサンプルサイズと確率β若しくは確率（1-β）の関係は、評価者は理解しておく必要性がある。
a） 第一種の誤りの確率αは検定する際の有意水準で一義的に決定する。
b） 第二種の誤りの確率βは母集団のパラメータ値により変化する。
c） αは小さく設定できてもβは非常に大きな値になり得る。
d） αを大きく（小さく）設定するとβは小さく（大きく）なる。
e） サンプルサイズを大きく取るとβは小さくなる。
3.4 両側検定と片側検定
仮説を立てる際は二つの仮説を並立するが、主役である対立仮説の「帰無仮説が誤りであった場合にどのような事が想定できるか」については、評価者が期待するいくつかの状態が設定できる。設定の仕方により検定方法（検定する方向）が異なるため、検定評価者はこれらを把握しておく必要がある。
a) 両側検定
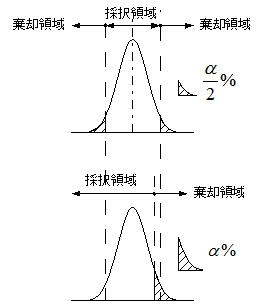
検定する差の方向は問わないで単純に差があるかないかを両方向で検定する場合に採用し、対立仮説の候補は不等記号（≠）のみである。有意水準（α%）は両側に均等に振り分けられるので、棄却領域は両側に設けられる。
b) 片側検定
特性の優劣など差異の方向を積極的に検出したい場合に採用する方法である。対立仮説は評価者が期待する方向により二つ（＞、または＜）あり所要の方向を採る。有意水準（α%）は片側（検定方向により上側または下側）のみに設定されるので、結果として棄却領域は両側検定より分布の内側に移動するため、両側検定よりやや厳しい判断が得られる。
3.5 仮説検定のタイプ
仮説検定では二つまでの母集団を扱うことができ、検定する母集団の母数に適用される統計量の分布からそれを冠する名称で呼ばれている。
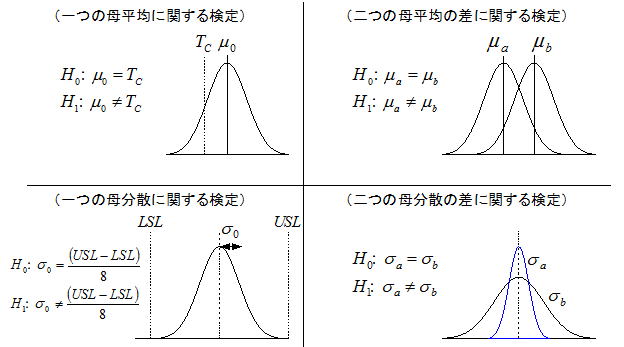
1) ｔ検定（一つの母平均に関する検定）
H0：μ0＝Tc H1：μ0≠Tc
2) χ二乗検定（一つの母分散に関する検定）
H0：σ0=(USL-LSL)/8 H1：σ0≠(USL-LSL)/8 USL：規格上限 LSL：規格下限 ※分母の8は工程能力Cp=1.3を意識した係数である。
3) ｔ 検定（二つの母平均の差に関する検定）
H0：μA＝μB H1：μA≠μB
4) Ｆ検定（二つの母分散に関する検定）
H0：σA2＝σB2 H1：σA2≠σB2
3.6 検定統計量
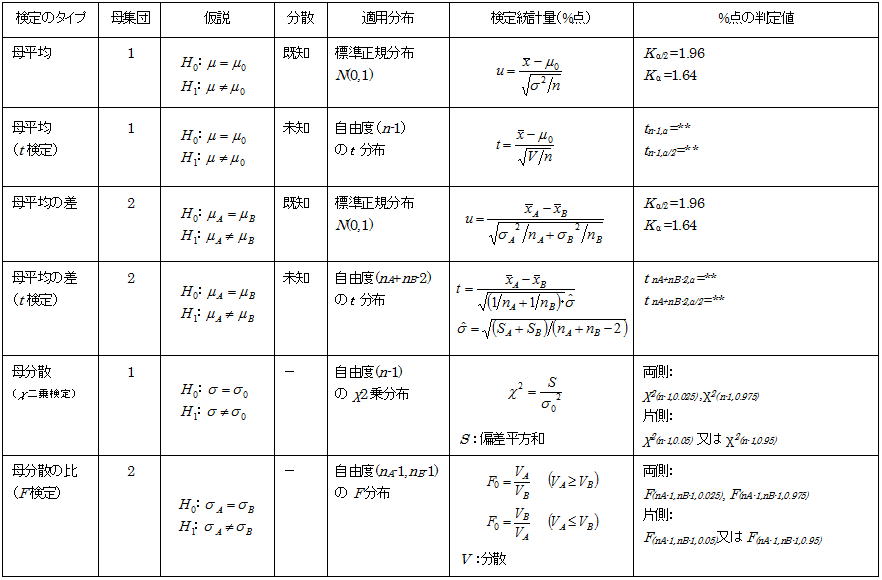
3.2項における判断基準を得るために何が必要かを考えてみよう。試料の統計量（平均、分散）がどの程度の確率で得られるかに関心があり、その比較対象は有意水準（α%）である。一方は統計量としてのある値（物理量）でもう一方は確率なので、両者を直接比較するには同じ尺度に変換する必要がある。仮説検定ではこの尺度に一般的に分布の%点を用いるため、統計量の%点と有意水準の%点（検定統計量）、及び統計量が適用される分布などが検定に必要な情報となる。以下の表に検定のタイプで適用される統計量の分布と検定統計量を示す。我々エンジニアは、統計解析を客観的な判断が得られる有効なツールとして利用（実践）はするが、”解析屋”になることが目的ではないのでこれらの情報を細かく知っておく必要はない。これらの情報処理はツールに任せて、検証結果をどう捉えるかだけに注力すればいい。
４．仮説検定の結果の捉え方
実践編にあるように統計解析ツールを使用すると何らかの結果（何れかの仮説が採択）が得られるが、判断決定の二つの誤り（リスク）が大きく異なるため、結果の捉え方（採択された仮説の信憑性が大きく異なることの認識）が非常に重要である。
1) H0が棄却された場合
サンプルサイズの大小に関わらず、意味のある差（有意差）があるとの判断ができる。この場合それを誤る確率は第一種の誤りであり、一義的に（検定の有意水準：通常は5%）に決まるためH1は積極的に支持できることになる。これが「仮説の主役は対立仮設である」との所以であり、6項の仮説検定のプロセスにおけるH1の考え方（立て方）に繋がる訳である。
2) H0が棄却されなかった場合
正しい結果である可能性も十分あるが、第二種の誤り（β）が高い確率である可能性もありH0は積極的には支持できない。H0の内容を積極的にいうためには、βの値が小さいあるいは検出力（1-β）の値が十分に大きいことを別途示す必要がある。つまり仮説検定でH0が棄却されなかった場合は、それのみでは明確な判断材料は得られないのである。
５．仮説の設定方法（工程能力指数との関係）
5.1平均値の検定
統計解析の文献の例題でよく見られるが、単純に試料統計量をある目標値（規格中心値：Tc）で検定しても得られる結論は目標値であるかないかだけである。この場合は正確さ、つまり母平均がある値より大きいか小さいかを問う行為であるが、工程能力指数のCpk （“正確さ”+精度）の検定と考えればよく、Cp →Cpk に変換する際のダウン率と考えれば更に分かりやすい。具体的にはCpk =(1-K)Cpより「Kの値がある値より小さい」事を問う仮説と考えればよく、仮に K < 0.1（ Cpの0.9以上）を問うことにするとKの計算式よりμを求め、その値以下になるように帰無仮説を立てればいいことになる。
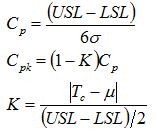
5.2分散の検定
仮説検定ではCpk（正確さ+精度）を同時に検定することはできないので、正確さと精度は別々に検定することになり精度の検定は「分散がある値より小さい」事を問う行為となる。精度の指標であるCpの値は一般的には1.3 を言われている（断っておくが全てにおいてこれを厳守する必要はない）ので、規格幅（ USL- LSL） に対し8σであるかがその判断になり、対立仮設としてその分散値より低いことを立てれば、母集団の工程能力（Cp）が1.3以上であることが検証できる。
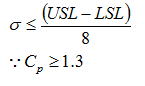
このように正確さ（Cpk）と精度（Cp）について具体的に検証することで、仮説検定の少し弱い部分（母集団をイメージしにくい）を補えば、仮説検定でも工程能力を十分に評価できよう。但し規格範囲外の不適合率がどの程度発生するかなどまでは及ばない。
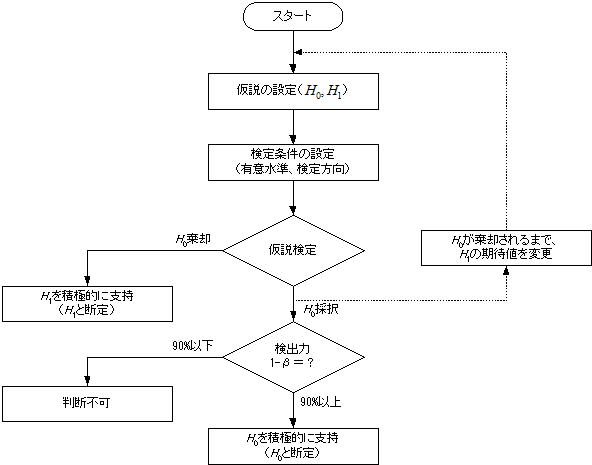
６．仮説検定のプロセス
検定プロセスを纏めると以下のようなフローチャートになる。2項で述べたように仮説の主役は対立仮説にあり、評価者は自分が期待すべき情報を先ずH1側に設定し、その内容を肯定する内容としてH0を並立する。検出力の判断（図では90%）は一応の目安であり、何れを採用するかはプロセスの重要度などにより評価者に委ねられる。”判断不可”とは検証の失敗を意味するが、これに至る主要な要因は試料数の不足である。エンジニアには元々豊富な工数と開発費（試作費）は与えられていないため、H0が採択された場合のリカバリは苦しいのが常である。なおH0が採択された場合は仮説検定の常套手段ではないが、統計ツールを用いることで直ちに結果が得られるので、棄却限界を探ることで期待すべき状況との差を確認（実践の頁を参照）できる。但しこの検証結果は評価者の裏取り作業であり、技術報告書に記載すべきことではない。
