

1.工程能力
工程能力は種々のプロセスが有する品質達成能力と表現され、この達成能力を数値化したものを工程能力指数という。具体的には製品品質や部品品質が、規格値(規格幅)に対し十分満足し得るかどうかの指標となるものである。的を狙って何本かの矢を放ち、下図のようになった場合を考えよう。左図はばらつきは小さいが的の中心(目標値)からのずれが大きく、一方右図は的の中心付近にはあるものの全体的なばらつきが大きい。
何れも不良発生率(規格外に落ちる確率)に影響することになるが、品質管理上の問題点としては後者の方が大きい。これは目標値からのずれは一般的には単純な原因である場合が多く、逆な観点では「原因の特定と修正が簡単である」と言えるが、一方全体的なばらつきは複数の要因が複雑に絡み合っている場合が多く、原因の特定と修正が簡単ではないことがその理由になる。
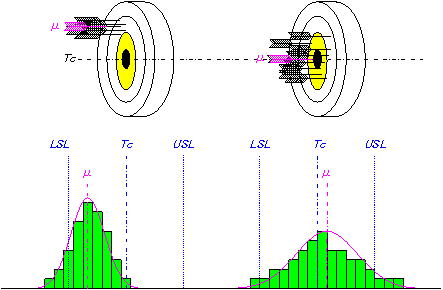
工程能力指数にはCpとCpkの二つがあるが、順序としては先ずCpありきとなる。これは前者はばらつき具合、後者は(ばらつき具合+目標値からのずれ具合)を数値化したものであり、Cpk≦Cpの関係となることによる。何れも、規格許容幅(USL-LSL)と評価アイテムの母平均(μ0)及び母標準偏差(σ0)で決定されるので、評価する際のパラメータは出来るだけ推定確度を高くする必要があるが、エンジニアが開発プロセスで扱える試料数はたかだかn =5~15個前後であり、エンジニアにとってはなかなか厳しい条件となる。しかし試料統計量で工程能力指数を評価することは、絶対に避けなければならない。
1) 両側規格の場合
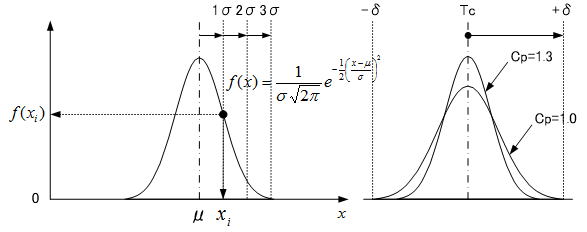
両側規格の各工程能力指数は以下の式で求められる。Cpは下図のように正規分布の6σ(±3σ)の範囲と規格幅の相対比であり、ばらつき具合(精度)を評価する指標となる。Cpkは式に示すようにCpに1以下の係数を掛けたもので、Kは目標値からのずれ具合を表す係数で式よりTc=μの時はK=0となるためCp=Cpkとなる。Cpがばらつき(精度)を表すのに対し、Cpkは「ばらつき+ずれ」(精度+正確さ)の指標となる。
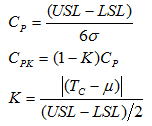
2)片側規格の場合
規格中心が存在しないのでCpkの概念はなく、上限規格と下限規格のCpは以下の式で求める。
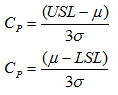
3)工程能力指数の安定性判断基準
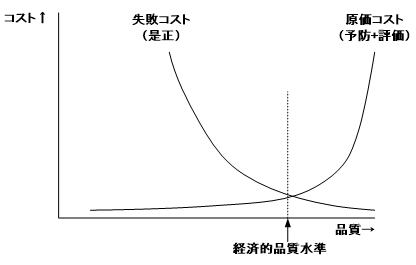
下表に工程能力指数の一般的な安定性判断基準を示すが、従来からの考え方であるCpk≧1.3はあくまで一般論としての目安であり、闇雲に全てのプロセスでこの基準を満たす必要性はない。エンジニアはなるべく経済的品質水準になるよう失敗(是正)コストと原価(予防+評価)コストを考慮し詰める(設計する)訳だが、コストバランスと工程能力指数のCpk≧1.3の条件が、全てのプロセスで折り合うとは限らない点がある。

2.公差解析
2.1概要
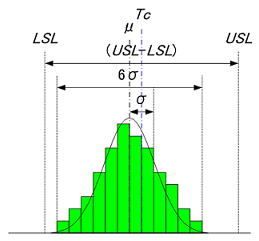
公差の基本的な考え方は、ある基準(目標)値に対するばらつきと誤差の許容範囲を与えようというものである。公差は許容範囲を示すものであるが、表面上はその範囲における確率的な解釈は示されてはおらず、単純に製造(加工、組み立て)検査(測定)プロセスにおいて、ばらつきをゼロにすることが不可能なため公差を付加するが、設計している当事者は必ずしも工程能力を意識しているとは限らない面がある。しかし確率的な解釈が統一されていないと、以降の展開(累積公差解析)が大きく異なってくるのでこの定義は重要である。目標値に対する偶然的に発生する変動(管理できない誤差)は、下図に示すような正規分布に従うことが論理的に証明されており、公差解析ではこの前提が重要である。部品のある寸法が正規分布と仮定でき、Tc±δを設計値とした場合を考える。ここで工程能力(Cp=1.0)を想定すると、平均値(μ=Tc)、標準偏差(σ=δ/3)の分布を仮定したことになり、公差内に入る確率は約
99.7%(不良率:0.3%)になる。公差(κσ:κ=3,4,5,~)のκについては一般的な指標であるκ=4(Cp=1.33:不良率は約 0.006%)が基準となるが、部品に求める機能(固有技術)、加工工程プロセス(設備能力、検査
の要否など)、部品コストなどを考慮した上で評価する必要がある。

2.2累積公差の計算方法
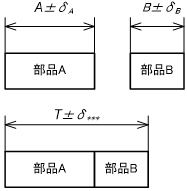
この考え方として従来から二つの計算方法があることが知られており、その一つは単純積算でもう一つは分散の加法性である。ポイントはこれらの方法の使い分けにあるが、他の統計的手法ツールと同様にこれをどう使い分けるかは、固有技術の観点から評価者が決定する以外にない。下図に二つの部品(A,B)における単純積算と分散の加法性による、累積公差の計算例を示すが、計算結果に示すように値自体は単純積算の方が大きくなる。
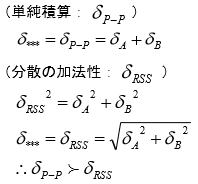
1)分散の加法性の適用
二つの母集団A,Bがあり、それぞれ正規分布に従うものとしその平均と分散は(μA,σA2)、(μB,σB2)としよう。これらの母集団から任意に抜き取られたサンプルを組み合わせた平均と分散は(μA+μB,σA2+σB2)の分布に従うが、この分散の関係を“分散の加法性”という。上図右に示した式は公差の値をそのまま用いて計算しているが、分散の加法性は本来は分散を用いて定義する方が望ましく、この場合は公差を工程能力指数(Cp)により分散(標準偏差)に置き換えて計算する。従って累積公差は、以下のように二つの定義が混在して使われる。
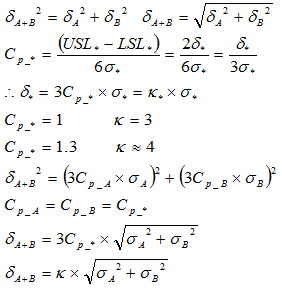
公差(κσ:κ=3,4,5,~)のκについては一般的な指標であるκ=4(Cp=1.33:不良率は約 0.006%)が基準となるが、部品に求める機能(固有技術)、加工工程プロセス(設備能力、検査の要否など)、部品コストなどを考慮した上で決定する必要がある。以上の定義により分散の加法性が適用できる事例は、母集団の分布が正規分布と仮定できる若しくはデータ検証により正規分布が明確な場合となるが、一般的な機械加工品(切削、板金、樹脂成形など)は既に多くの実績(事例)があり、これらについては正規分布を仮定できない有力な根拠は見当たらない。
但し実績データが全くない部品(新しい製造プロセスによる加工部品など)については、 工程能力などの評価を実施する際にヒストグラムを作成し歪度と尖度の値により、正規性を確認することが推奨される。
なお正規分布と仮定できる場合でも、機能維持 (固有技術の観点)のための判断が優先される場合はこの限りではない。
2)単純積算の適用
単純積算の適用は言い換えると分散の加法性が適用できない場合の対応であり、更にその理由に遡れば母集団の分布が正規分布と仮定できないことになる。このような場合としてどの様な状況が考えられるであろうか。容易に気付く例として検査工程を経た選別部品などがあるが、何れにしても自然発生的ではないばらつき要素が含まれる懸念がある工程部品については、単純積算を適用すべきである。
2.3確率的解釈(不良率の推定)について
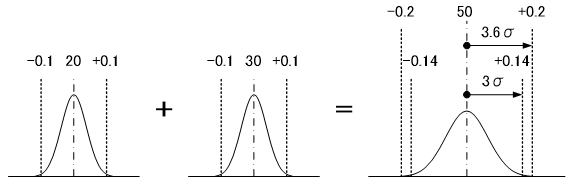
累積公差の計算方法の違い(単純積算と分散の加法性)による、公差範囲外が発生する確率 (不良率)について考える。 但し正規分布と仮定できない場合はその推定が非常に困難となるため、各部品の公差は正規分布と仮定できるものとする。説明を簡単にするために、下図の二つの部品の組合せ例における工程能力を1.0とした場合の、上限公差を外れる確率を考える。


先ず何れの場合でも二つの部品が上限公差( +0.1)外になる確率は、工程能力1.0(δ=3σ)の確率より約 0.13%と推定される。単純積算における確率は直列系の不信頼度と同様に考えればよく、累積公差上限(+0.2)を外れる確率は0.132=0.0169%と推定される。一方分散の加法性では累積公差上限(+0.14)を外れる確率は誤差伝搬の法則が適用されるため、部品の上限公差外となる確率0.13%がそのまま反映される。
次にこれらの確率(不良率)の%点(平均値からの距離)を考えると前者は3.6σ後者は3.0σの確率に相当し、つまり単純積算では不良率を低く見積もる事はできるが、累積公差が拡大するため設計余裕は厳しくなるのに対し、分散の加法性では不良率は若干大きく見積もられるが累積公差は縮小するため、設計余裕(確保)については柔軟性が増すことになる。
3.実施例
3.1工程能力が不明な場合
下図に示すような切削加工品(A,C)と樹脂成型品Bを組み合わせた際の累積公差(δT)を解析する。なおκ=3(つまり工程能力Cp=1)とする。
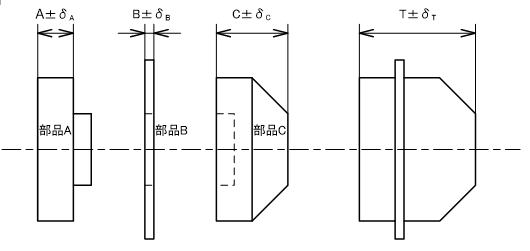
累積公差(δT)は以下のように求められる。なお累積公差を決定する際のκは基本は標準偏差を推定した際の値を用いるが、不良率をどの程度見込むかにより適宜変更してもよい。
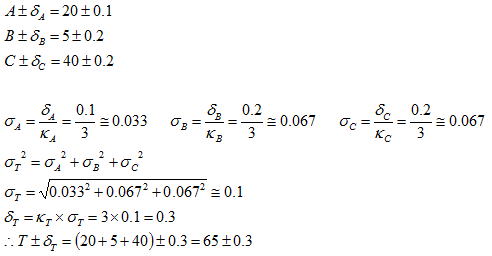
3.2工程能力が既知の場合
3.1項と同様な部品構成で、各部品の工程能力が既知の場合の累積公差(δT)を解析する。累積公差(δT)は以下のように求められるが、累積公差を決定する際のκTは各部品の工程能力が異なっているため便宜的にκT=3としたが、3.1項同様に適宜変更してもよい。
部品A:Cp=1.2
部品B:Cp=1.1
部品C:Cp=1.3
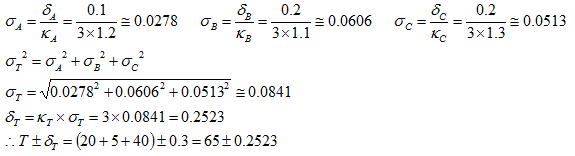
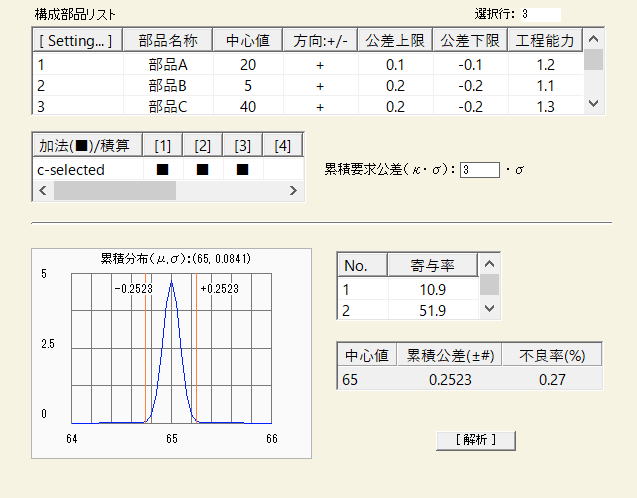
●SA&RA ProXによる解析
同じ例題によるSA&RA ProXによる解析結果を示す。累積公差として同じ値が得られていることが分かる。
3.3直角度と平面度の扱い
直角度や平面度は見掛け上公差範囲のみが示され、設計寸法としての中心(目標)値は示されない。このような場合は中心値を0とした両側公差に変換して計算する。例えば平面度の指示値が0.1の公差は0±0.05として解析する。
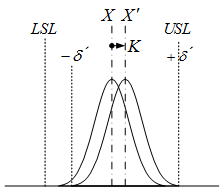
3.4片側公差の場合(±公差で等しくない場合)
片側公差を両側公差として均等に振り分け中心値は見掛け上の中心値とする。予め工程能力(Cpk)のK値(言い換えると目標値からのずれ)が既知で、且つ分散が許容範囲(目安:C
pk ≧1.0)の場合も同様に扱える ものとする。以下にそれらの例を示す。
1)±公差で等しくない場合
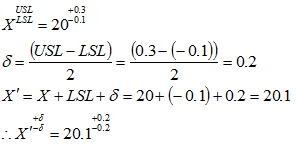
2)K値が既知の場合で且つCpk≧1.0の場合
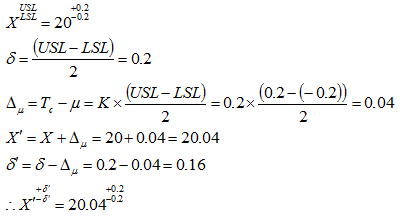
4.纏め
公差解析の最大のポイントは、累積公差の計算方法で何れ(分散の加法性と単純積算)を選択するかであろう。但し2.2項で述べたようにこの選択は固有技術の観点から評価者が決定する必要がある。公差と工程能力は直接的に関係するため、所要の組み合わせ公差を得るに際しては各部品の要求機能(品質若しくは信頼性)とコストを常に念頭に置いて、組み付け部品の公差配分を検討する必要がある。2.3項で公差を外れる確率(不良率)について述べたが、一般的に公差を厳しくすると高精度の加工(加工工数が増大)を必要とするためコストは上昇する。