

1.概要
一般的に電子機器の寿命は、機械製品のように時間の経過に伴って進行する摩耗系故障を持たないので、一定時間経過後の故障モードを特定できるケースは非常に稀で、信頼性試験を行っても故障が発生することは殆どなく、信頼度を直接評価するための情報は得られにくい。従って電子(電気)技術者は機能・性能が満たされれば相応の信頼度はそれに付随すると考え、妥当性確認試験(一般的な条件よりやや厳しい環境(湿度・温度など)での一定時間(例えば1000hr~程度)の連続通電試験など)で信頼性の評価を終えることが多い。しかしこの期間に発見される故障は長期的な信頼性とは明らかに母集団が異なるため、後者は別な次元で評価する必要がある。電子機器の信頼度予測はこの情報が得られる有力なツールで、巧く活用すれば信頼度の改善活動にも繋げられる強力な手段にもなる。これは信頼度予測のプロセスにおいて、部品に印加されるストレス(周囲温度、電圧、電流など)などが適正レベルであるか検証されることによる。更に最近の市場要求は「機械・設備の安全性評価と信頼性データ」において示したように、機械・設備に使用される機器の寿命は定量的に示すことが求められており、この観点からも電子機器の信頼性設計プロセスに不可欠なものである。
2.信頼性の尺度
電子機器の信頼性評価で用いられる一般的な尺度は、単位時間あたりの故障数(故障率)と平均故障間隔(電子機器は一応修理系なのでMTBFで表現するものとする)であるが、これは電子機器の寿命特性(故障密度関数)が指数関数に従うことによる。故障率の単位は最近は109時間あたりの故障発生数(FIT:Failure In Time)が主に用いられ、109時間(10億時間)で故障が3個発生した場合は3FITと表現される。平均故障間隔(MTBF)は機器全体のFIT値より求めることができる。
3.予測のための数理
扱う関数は指数関数に限定されるためワイブル分布(摩耗系に適用される分布)などと比較するとシンプルで、その確率密度関数は以下のように表せる。
![]()
ある時間までに故障する確率(不信頼度関数)と信頼度関数は以下のように表され、指数分布では- tの領域はないので0から積分することになり、式から部品の故障率(λ)が分かれば一定時間経過後の信頼度(不信頼度)は、以下のように推定することができる。
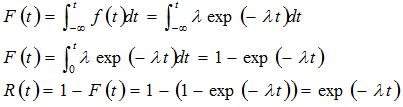
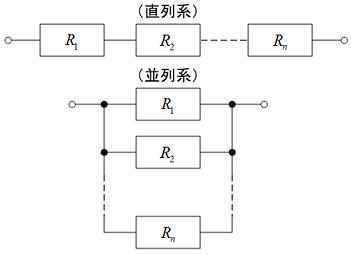
電子機器の故障率と部品故障率の関係は、一般的な機器の信頼度は直列系(冗長性を持たない)が適用できるため機器全体の故障率は構成部品の故障率を合計したものとなり、この考え方は部品点数法と呼ばれる。冗長性を有する機器の場合は並列系の部分の信頼度を以下により計算する必要があるが、一般的な電子機器の構成では並列系は考慮しなくてもいいように思われる。
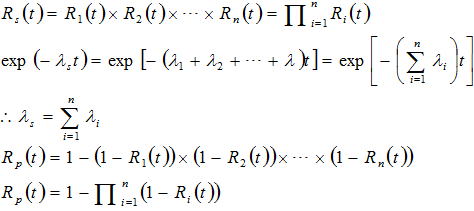
4.指数関数のMTBF
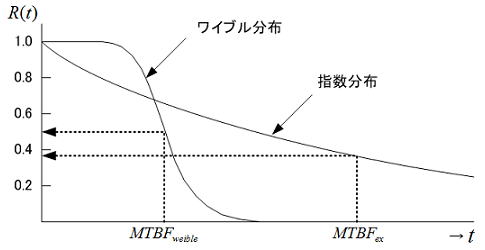
電子機器の信頼性評価では平均故障間隔(MTBF)がよく用いられるが、指数関数分布は論理的にはt は無限大まで分布するので、MTBFにおける故障確率は摩耗故障などにおける分布と比較すると、不信頼度はF(t)=(1-0.37)=0.63と少し大きくなることに留意する必要がある。一見すると指数分布の信頼度特性はt≧0から直ぐに低下傾向になるため、他の分布(この例では正規分布に近いワイブル分布)より悪いように思えるが、電子機器の信頼度の低下率は時間軸に対して非常に緩やかな分布になるため、バスタブ曲線の摩耗故障領域に至る以前の偶発故障領域と捉えれば分かりやすい。信頼度関数が指数関数で与えられるとその平均値(MTBF)は以下のように導かれるので、機器全体の故障率が分かればそのMTBF
も推定可能になる。
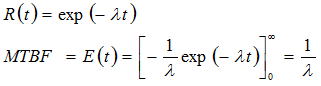
5.電子機器の信頼度予測の歴史
電子機器の信頼度予測の歴史は真空管の寿命信頼度を予測することから始まったと言われており、それ程長い歴史がある訳ではない。ここでは公表されている代表的な三つを取り上げて簡単にその経緯と内容を説明する。
1)MIL-HDBK-217#
本格的な最初の予測法として米国国防省が1962年度に制定したもの(MILハンドブック)で、従来の手法が部品の故障率のみで評価していたのに対しフィールドの故障率を基に部品の基礎故障率を決定し、設計条件や使用条件の影響を考慮(補正)するための部品ごとのモデル式の導入などにより予測信頼度は格段に向上した。簡易な「部品点数法」と詳細な「部品ストレス解析法」があり、何れの方法もモデル式を用いて故障率を計算するのは同じであるが、前者がストレスを標準的な条件に固定しているのに対して、後者は任意のストレス条件で計算するため前者より故障率の推定確度が高い。1995年に改訂(-217F
Notice2)されて以降改訂されていないため、現在では基礎故障率のデータがない部品も多くなっているが、その後に開発された予測法はこの規格が原型といっても過言ではない。
2)Telcordia SR-332(Bellcore)
1995年以降MIL-HDBK-217が改訂されなくなり、その代替え手法としてBell Communication Researchから「Bellcore
TR-332」が発表された。但し現在ではTelcordia Technologies,Incから「Telcordia SR-332」として公開されている。内容的にはMIL-HDBK-217の二つの方法(部品点数法と部品ストレス解析法)の中間的な手法であり、ツールとしての操作性は比較的簡便ながら推定精度は一定レベルを維持できるものになっており、定期的に改訂されているため情報の鮮度も問題はない。なおSR-332でははんだ付けの故障率は0と査定されるため、精度を上げるためにはこれを含める必要がある。
3)PRISM
MIL-HDBK-217に代わるものとしてSR-332が発表されたが、予測精度がやや低いこともあり高い予測精度に応えられる手法として開発され、米国国防省の外郭団体である信頼性解析センター(Reliability
Analysis Center)により開発された最新の予測法である。高い予測精度を得るためモデル式はかなり複雑であるが全ての部品にモデル式が与えられている訳ではなく、モデル式がない部品についてはフィールドデータが掲載されている。モデル式が複雑なため解析するための専用ソフトが開発されている。
4)IEC規格
1996年度にIEC1709:Electronic Components-Reliability-Reference conditions
for failure rates and stress models for conversionが制定されているが、電子部品の故障率モデルとストレスファクタが示されている。本規格では部品故障率そのものの値は示されていないが、ストレスファクタの考え方は参考になる。
6.MIL-HDBK-217Fの予測法
6.1部品ストレス解析法
部品点数法より高い精度が得られるが詳細な技術情報(使用部品の電圧、電流、周囲温度、使用環境など)が必要なため、部品選定の初期段階では適用できない。基本的な考え方は部品毎に異なったモデル式を定義し、部品アイテム毎の基礎故障率を各ストレスに応じて対応するπファクタと呼ばれる係数で補正し故障率を求めるものである。πファクタには共通的なものと固有なものがあり、部品毎に適用されるπファクタが定義されている。例えばトランジスタ(低周波・バイポーラ)のモデル式は以下のように定義されており、以下各πファクタについて説明する。
![]()

1)部品基礎故障率
部品単体での故障率であり部品カテゴリごとに決める必要があるが、市販電子部品のカタログスペックとして掲載されている訳ではないので、自前のフィールドデータが揃っていない場合は基礎故障率の情報収集は意外と困難である。一つの手立てとして既に公開されている予測法のデータを適用することが考えられるが、カスタム部品(例えばセンサー、カスタムICなど)は自前でフィールドデータなどから決定する必要がある。
2)温度ファクタ
T (部品のケース温度など)とEa(部品固有の有効活性化 エネルギー)により下記式で求められ、例えば Ea =2100であれば周囲温度60℃であるなら![]() となる。
となる。
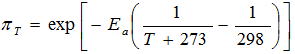
3)適用ファクタ
用途によるファクタで例えば(低周波・バイポーラ)では、増幅器とスイッチングの2水準がある。
4)定格電力ファクタ
素子の定格損失の大小による故障率の重み付けで定格損失が大きい素子程πファクタ値が大きく、例えば100mW以下では0.43であるのに対して100Wでは5.5の値になる。
5)電圧ストレスファクタ
例えばトランジスタではコレクタ最大定格に対する印加電圧の水準レベルで決められており、概略以下の値に設定されている。
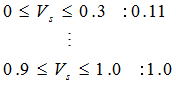
6)品質ファクタ(共通ファクタ)
部品の故障率は同じ定格(種類)のものであっても同じ故障率になるとは限らず、設計から製造までの各プロセス(平易には部品メーカーの品質管理レベル)に応じた故障率になるため、部品アイテムとプロセスの品質レベルに応じて補正係数が与えられている。
7)環境ファクタ(共通ファクタ)
機器の故障率は使用環境(設置環境)により変化するので、それを補正するためのファクタ(πE)である。

6.2部品点数法
部品ストレス解析法の簡易法でこの方法では各種のストレスは考慮せず、部品アイテム毎に決定された故障率をそのまま利用して推定する。故障率はストレスをある標準状態(温度ストレス:部品により30℃又は50℃、電気ストレス:40%)の値に設定して計算されており、その際のモデル式は部品ストレス解析法と同じ式のため基本的な考え方は変わらない。この方法では部品が選定されれば信頼度を推定することが可能で、精度はストレス法より劣ることは否めないが設計の初期段階で信頼度を推定することができる。
7.Telcordia SR-332の信頼度予測法
基本的にはMIL-HDBK-217Fの流れを汲むもので、全部品共通の故障率モデルにより部品ストレス解析法よりかなり簡易であるが、設計条件や使用条件を反映できる各ストレスファクタの補正により推定精度は悪くはなく、何よりツールとしての操作性(簡便性)がいいため、この手法を適用するメーカーは多いと思われる。
1)故障率モデル
MIL-HDBK-217Fの故障率モデルは部品アイテムにより多少異なっているが、SR-332では全ての部品に共通なモデル式になっている。
![]()

2)品質ファクタ
MIL-HDBK-217Fに比較すると最下位レベル(0)の値が大きいが、この値が採用されることはないと考えられる。

3)電気ストレスファクタ
以下の式で表され基準ストレス(50%)ではMa値に関係なくπS=1.0 となり、調整パラメータMa(0.002~0.059)は部品アイテム毎にそのランク値が決定される。
![]()

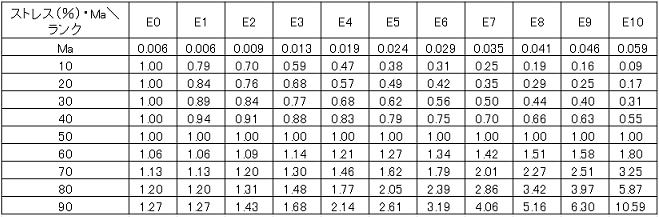
4)温度ストレスファクタ
温度ストレスファクタは部品の周囲温度(T)と部品アイテム毎の活性化エネルギー(Ea)により決定され、周囲温度は40℃が基準値で以下の式で表される。活性化エネルギーEa(0.05~0.7)はストレスファクタ同様に決定される。
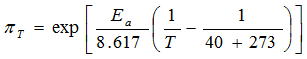
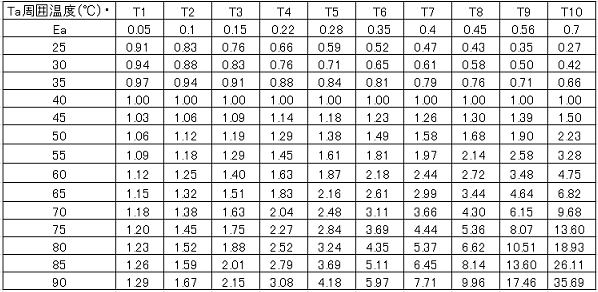
5)環境ファクタ
SR-332では部品故障率のモデル式には含まれていないが、機器の予測時に纏めて補正を行う手法を取っている。環境ファクタの水準とファクタ値はMIL-HDBK-217Fと殆ど変わらない値に設定されている。
8.信頼度予測法の構想
1)予測の推定確度
電子機器の信頼度予測は部品の基礎故障率を決定する際にフィールドの実力値は反映されるが、ワイ ブル解析(実際の故障データを用いる)のように母集団そのものを明確に示すものではなく、更に設計条件(熱設計、設計マージンの確保など)に応じて正確にπファクタを照合させることにも限界があり、従っていく
らかの誤差は許容すべきものと考えなければならない。実際のフィールドデータとの照合は簡単ではないが、許容できる誤差の範囲は実力値と±20%程度と考えられる。予測値と実力値が一致しない理由の云々より、評価者が常に同じ尺度で評価(目標値あるいは従来モデルや競合モデルとの比較)できることが重要で、信頼度の予測精度を向上させることは使いながらノウハウを蓄積する
ことで十分可能である。
2)予測法の選択
予測の難易度(手間と使う側の技量)と予測の精度は逆の関係にあり、予測の難易度は以下の順で難しくなり一方得られる予測の精度はその逆の順になる。何れの手法も一長一短があるが信頼度は設計者自らが行うことが望ましく、その観点からは専門知識がある程度必要なPRISMは難があり、電子機器の信頼度予測に初めて取り組むのであれば管理人は難易度と精度のバランスがいいSR-332を推奨する。
①MIL-HDBK-217F(部品点数法)
②SR-332
③MIL-HDBK-217F(部品ストレス解析法)
④PRISM
3)基本仕様
先ず部品基礎故障率を公表されている規定など(MIL-HDBK-217F、SR-332、PRISMなど)を参考にデータベース化し、他の要素としては接続部(プリント基板(スルーホールを含む)、はんだ付け、コネクタ部など)の故障率も考慮する。データベースにない部品(カスタムIC,センサなど)については、任意の値(故障率・各πファクタ)を入力することで取り込み可能にする。部品基礎故障率表(データベース)を兼ねた計算ワークシート(EXCELファイル)を作成し、フォーマットに従って条件を入力すると条件に応じて部品毎の故障率~機器全体の故障率が計算され、信頼度(MTBF)が求められるようにする。
補正πファクタはSR-332と同様の以下の4ファクタを取り上げる。
πQ:品質ファクタ(共通ファクタ)
πE:環境ファクタ(共通ファクタ)
πT:温度ファクタ(基準温度:40℃)
πS:ストレスファクタ(基準ストレス:50%)
9.信頼度予測ワークシート(EXCEL版)
8項の構想仕様をEXCELシートに纏めると以下のようになる。部品アイテム毎の分類により個々の部品の故障率が決められており、部品毎に適用する温度ストレス曲線と電気ストレス曲線が選択されている。この項目までは部品毎に値が決められており、残りの設計要素に値を入力することで部品個数に応じた故障率が計算される。全ての故障率(FIT)が集計されたら、以下によりMTBF(時間及び年単位)が求められる。

〇一般的な電子機器の入力例
環境ファクタ:1.0
品質ファクタ:0.8(国内生産部品は一律この係数でOK)
周囲温度(温度ストレス):50~65℃(一般的には機器の作動中における筐体内部温度を反映させる)
設計マージン(電気ストレス):30~70%(使用素子の最大定格に対する設計マージンを反映させる)
![]()
電子機器の信頼度予測ツール(信頼度予測ワークシート(EXCEL版))の入手につきましては、「➡統計解析・信頼性解析ツール(SA&RA ProX・EXCEL計算シート)」を参照下さい。