

1.概要
信頼性工学は機械系、電気(電子)系の両分野にまたがり、その裾野は非常に広大である。但し一般的なエンジニアにとっての信頼性とは、単純に自分が設計した製品が所定の期間まで故障しないことである。設計プロセスにおいて設計者は機能設計と信頼性設計の両面から製品を設計し、この内前者は設計検証、後者は妥当性確認(信頼性試験)で検証することになる。後者を担う主要なツールとしては二つが挙げられ、それは設計FMEAと信頼性解析である。ここではエンジニアにとって最もポピュラーな、機械構成機器(電気機器を含む)の摩耗系故障の信頼性解析について述べる。機器の信頼性とは具体的に何であろうか。統計的な表現では「固有のアイテムが一定の条件下で所定の期間、要求機能を満たすことができる能力」となるが、簡単には「故障が起きない確率」と思えば分り易い。統計解析も信頼性解析も得られたデータに基づき母数のパラメータを推定する行為は同様であるが、前者が主に正規分布と仮定した上での論理に対し、後者は仮定される分布が正規分布と限らない点、及び故障寿命(時間)データは順序統計量として扱う点などが異なる。解析する上で理論の理解は全く不要とは言わないが、信頼性工学の理論を熟知する事が我々の目的ではなく、自分が設計した製品の信頼性がどのようにすれば設計審査において定量的客観的に示せるかであり、その範囲は概ね以下の通りである。
1)完全データ及び定時(定数)打ち切りデータの解析(ワイブルチャートによるグラフィック解析)
2)不完全データ(故障数0個を含む)の解析
3)所定の信頼性特性値(B10、MTTFなど)を証明するための最短試験規模
4)ワイブル分布の計数1回抜き取りLTFR(Lot ToleranceFailure Rate)方式
当管理人は、”空気圧-試験による機器の信頼性評価”ISO19973-1/JIS B8672-1の編集員に携わった経緯があるが、この規格の内容はほぼ上の内容を網羅しており、制定時点ではこのような内容の規格は他になくかなり画期的であった。
2.信頼性評価と母集団
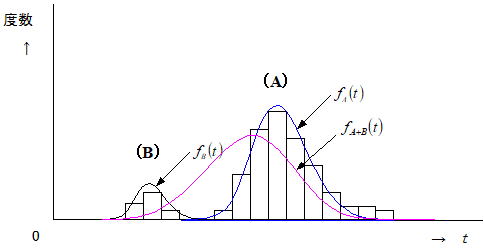
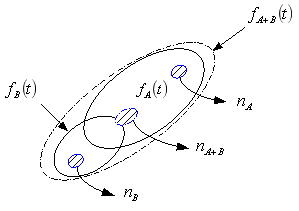
不適合的に発生した事象でない限り、顧客を含めて我々が最も知りたい製品の寿命は、「ある標準」が遵守された”真っ当な寿命”である。ここで問題なのが「ある標準」の定義で、基本的には取り上げる試験因子とその水準により決まるが、信頼性データにおける母集団の範囲は、製品、動作条件、環境条件、故障モードなど多岐に及ぶため綿密な検討が必要である。信頼性特性値(信頼度、故障率、故障強度、平均寿命(MTTF,MTBF)、B10ライフなど)が母集団を代表していることが重要で、定義が曖昧な試験から得られた信頼性特性値は、本来知りたい寿命とは異なる可能性が高い。ある製品のフィールドデータを取得し、時間軸に対するヒストグラムが下図のようになったとしよう。フィールドデータはこのようなデータ(複数の分布が混在)になる傾向があるが、下図のような度数分布が得られたとき、二つの分布をどう考えればいいだろうか。我々は(A)分布のような一定のばらつきは容認しているが、(B)分布は同一の母集団から得られたとは考えにくく、異なる母集団(寿命加速因子の影響など)から得られたと考える方が自然である。これを同一の母集団として評価すると、本来の故障分布はfA(t)である可能性があるのに、fA+B(t)として評価される(つまり実際の分布よりばらつきが大きく見積もられる)可能性がある。前述したように母集団の範囲は多岐に及び、又生産者側、消費者側の母集団も異なるため、信頼性特性値を比較対象として扱う場合は特に注意が必要である。これを防止するには、元々の試料nA+BをnAとnBに分けて(この行為を層別という)別の分布として解析する必要があるが、管理人の経験からいえば殆どの場合評価者側での行為は困難である。信頼性特性値を比較する場合は、母集団の範囲について特に注意を払う必要がある。
3.データの種類
信頼性試験に携わった経験がある人は直ぐに分かることであるが、信頼性試験には大きな二つの壁がある。その一つは時間でありもう一つは数(コスト)である。特に前者については、投入試料数が全数故障に至るまで相当な時間(長いものではゆうに1年を超える)を要するため往々にして途中で打ち切られることが多く、全数が故障に至るデータ(これを完全データという)はむしろ稀である。従って信頼性試験では下図に示すような不完全データ(定時打ち切り、定数打ち切り、ランダム打ち切り)を扱うことが多い。
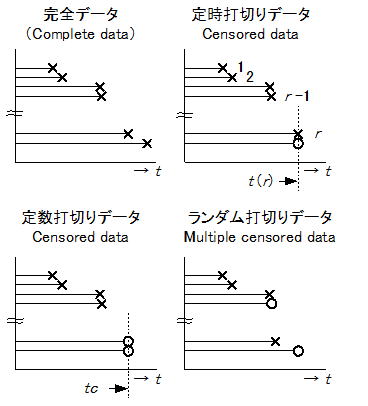
n個のサンプルサイズで信頼性試験を行い、n個の故障発生時間が観測された場合を完全データという。しかし前述した理由などにより全てが故障に至ることは稀で、信頼性試験の殆どは上図に示すような不完全データになり、定時打切りデータでは故障数0個のまま打切りになるものも含まれる。信頼性解析に用いられるデータは、信頼性試験により得られたライフデータとフィールドデータに大別されるが、我々が信頼性解析で扱うデータは殆どの場合前者である。管理人の経験では、フィールドデータは顧客の使用条件(設備稼働条件など)が異なるため、2項に示したような複数の分布が混在する場合が多く、殆どの場合それらを層別(母集団の違いを特定し別々の分布として扱う)することは困難である。なお前述したISO19973-/JIS
B8672-1では、試料数(n ≧7)と故障数(r ≧ n×70%)が定義されており、データの分類では定数打切りデータとなる。
4.解析に必要な数理
統計解析では正規分布の数理と関連する分布を理解しておけば事足りたが、信頼性解析では扱う数理(関数)も増え少し複雑になる。確率を論点とする基本的な考え方は、統計解析における種々の考え方と同様であるが、信頼性解析では故障が起きる(若しくは起きない)確率が信頼性の尺度となるため、この確率を定量化するための関数導入が必要不可欠になる。但し機械構成機器の摩耗系故障に限定すれば、以下の最低限の関数の導入だけで取り敢えずは十分である。
1)確率密度関数
ある製品のランダムサンプル(この例では25個)をライフ試験に投入し、ライフ試験データから下左図のようなヒストグラム(時間-度数分布)が得られたとしよう。仮に試料数を無限に増大させヒストグラムのセル幅を微小幅に狭めると、その頂点は滑らかな曲線になることが予測される。この内側の面積を1(確率で表現するなら100%)とするような分布f (t)を確率密度関数という。すなわち我々が求めようとしている母集団の分布であり、仮定された分布の母数を求める行為が信頼性解析となる。
2)不信頼度関数
確率密度関数f (t) における微少時間幅 dt を考えると、t ~ t+dt の間に故障する確率は f (t) dt と表せ、時間 tiまでに故障する確率は時間t=0 から t=ti まで f (t) dt を加えたものになり、これを不信頼度関数 F (t)という。ヒストグラム領域では累積度数の割合の上昇特性と一致するカーブになる。つまり式の上ではある時間における不信頼度F(ti)を得るには、母集団のf (t) が分かっている必要がある。
![]()
3)信頼度関数
不信頼度関数を用いて、時間 ti まで故障しない確率を表したものを信頼度関数R(t) という。
![]()
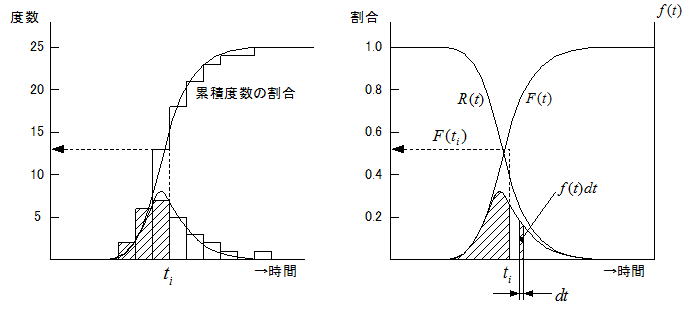
これらの関係を纏めると上右図のような関係になる。不信頼度と信頼度は一定期間経過後に0.5の位置で交差し、時間の経過に伴い前者は1後者は0に漸近する。エンジニアの最大関心事は、不信頼度の立ち上がりがいつになるか(摩耗故障はいつから発生するか)であろう。
5.信頼性特性値(MTTF:mean time to failure、B10)
5.1 MTTF
今n個のライフデータが得られたとすると、平均故障時間は単純に以下の式となる。
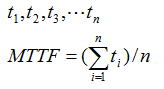
観点を変えて度数分布から平均値を考えるものとする。時間セルの中心値と各セル単位の発生度数を以下とすると、平均値は以下の式で求められる。各項を見ると故障時間(ti)にそのときの故障確率(割合:ni /n)を掛けそれらを合計したものと捉えることができ、平均値の推定量は最後の式で表される。
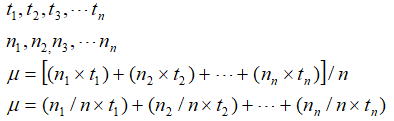
![]()
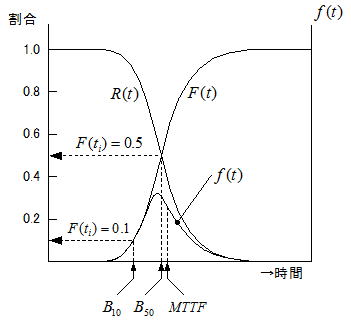
ここで不信頼度と信頼度の交差点F(t)=0.5の時間を考えてみよう。仮に正規分布と仮定するならその確率0.5(50%)の位置は平均(μ)と一致するため、t =μ=MTTFとの論法が成り立つ。しかし上図のように正規分布でない場合は、F(t)=0.5すなわち確率50%の%点(時間)と分布の時間軸上にちらばる各故障時間の平均値(MTTF)は一致しない。F(t)=0.5の時の寿命をメジアン寿命といいB50と表すが、故障分布の多くは左右非対称のためB50≠MTTFとなる。但し機械構成機器の摩耗系故障は、管理人の経験からはm≧4~6のほぼ正規分布に近似の分布となる傾向があり、一致はしないものの大幅にズレることはない。エンジニアの最大関心事である不信頼度の立ち上がりを捉えるための寿命をB10ライフというが、この説明は5.2項で行う。
5.2 B10ライフ
B10ライフは全体の10%が故障する時間(動作回数など)を言い、不信頼度 F(t)=0.1 (R(t)=0.9) における時間 t のことである。元々の語源はベアリングメーカーが自社のベアリングの寿命を表す際に用いた記号である。例えば50個のサンプルをライフ試験に投入し、下左図のような時間タイミングで故障が発生したとすると、全体の10%すなわち故障数が5個になった時間をいう。メンテナンス(交換)時期の目安となるもので、この意味合いから摩耗系故障を有する機器に適用されることが多い。B10ライフで評価する最も大きな理由は、信頼性のばらつきを考慮して評価することにある。下右図に示すように平均値(MTTF)はほぼ同時間位置にあるが、分布のばらつき具合が異なる二つの分布fA(t)、fB(t)を想定する。
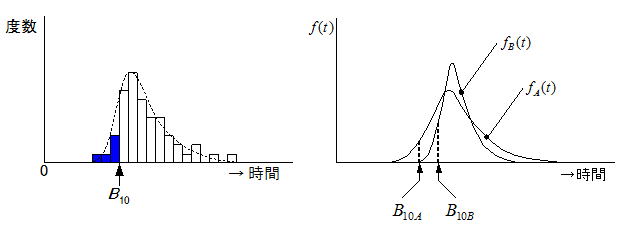
MTTFの評価ではMTTFA≒MTTFBなので信頼性は同等との評価になるが、最初の故障発生時間はfA(t)の方が明らかに早くB10ライフでの評価ではB10A<B10Bとなり、fB(t)の方が良い(寿命が長い)との結論となる。前述の規格(ISO19973-1/JIS B 8672-1)ではB10の片側95%信頼限界を評価基準として定義している。
6.分布の仮定
信頼性試験などの寿命データから信頼性特性値(B10 ,MTTF など)を得るには、分布が特定(仮定)されていなければならない。しかし統計解析では調査したい母集団の分布に対して、わざわざ「正規分布と仮定する」などとはいわない。これは仮説検定や推定の論理は母集団の分布は正規分布に依存することが前提となっており、敢えてそれをいわなくてもいいからと思われる。しかし信頼性解析では仮定した分布により得られる結果が異なるため、分布の仮定は重要である。分布を特定するための確率密度関数にはいくつかの未知の母数が含まれており、信頼性解析はこれらの母数を求める行為といえる。実施する上で文献には多くの関数の例が挙げられているが、機械構成機器(電気機器を含む)の摩耗系故障を扱う限り下式で表せる2母数ワイブル分布でほぼ代表できる。文献には母数がもう一つ追加された3母数ワイブル分布の例も挙げられているが、この母数(γ:位置パラメータ)は故障が何時から始まるかを表しており、バーンイン操作(いわゆるヒートラン試験と思えばいい)などを行った場合の補正に用いられる。この操作が必要な機械構成機器は特殊なものといえるので、通常はγ=0と置いた2母数ワイブル分布で解析しても問題はない。
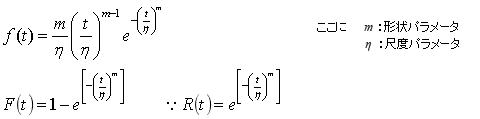
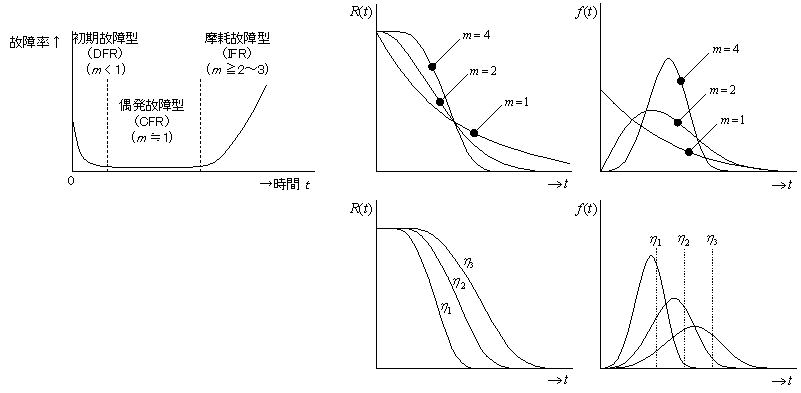
勿論2母数ワイブル分布で全てを代表できる訳ではないが、ワイブル分布はバスタブ曲線における何れの時間領域にも適用でき、故障分布の当てはめ性が良い(適用性が広い)ことが知られている。式から分かるように二つの母数(パラメータ)を持ち、m, η が決まれば変数 t によりワイブル分布は決定する。形状Par. m は分布のばらつき具合(分散)を特徴付ける母数で、尺度Par.ηは時間軸の尺度を決定する母数になり、パラメータの変化に対する分布(信頼度、故障確率密度)の振る舞いは下図のようになる。誤解を恐れずにいえば、前者は正規関数の標準偏差(σ)に該当し、後者は平均値(μ)に該当すると思えば分り易い。前記したように機械構成機器の摩耗系故障はm≧4~6のほぼ正規分布に近似の分布となる傾向がある。数理的には摩耗故障型(IFR)のm値はm≧1.0であるが、m≦2~3の確率密度関数の立ち上がりはほぼt=0から始まるため、このような製品は摩耗系故障を有する製品では存在しないと考えてよい。仮に解析結果としてm≦2~3が得られた場合は故障モードが摩耗系でない可能性もあり、それが当初予測された範囲であるかを含め設計的な要因なども検討する必要がある。
7.ライフデータの解析
7.1故障数がある(全数若しくは70%以上)場合(ワイブル解析:メディアンランク回帰法)
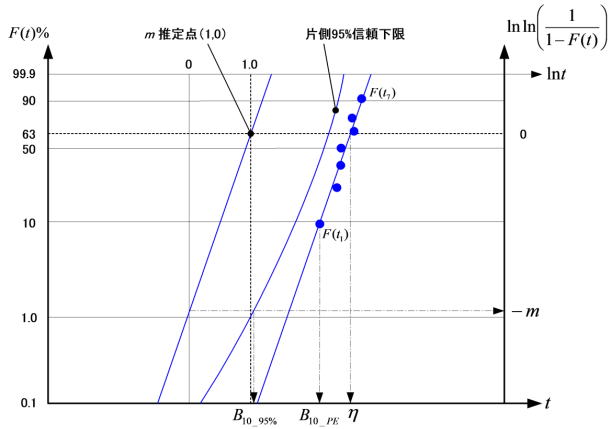
一定の試料数(n≧7個が望ましい)をライフ試験に投入しその全数が故障、若しくはその70%(概ねであり厳格に考える必要はない)以上が故障に至った場合に適用できるツールとなる。この場合の解析結果は、ほぼその製品の信頼性の実力値が得られると考えて差し支えない。この方法は、統計解析における回帰分析(二つの変数の関係を明らかにする手法)と同様で、ここでの二つの変数とは時間と故障が起きる確率(不信頼度)である。これを二つの軸(x,y)の平面座標にプロットすることで、時間と不信頼度の関係を明らかにしようというものである。各故障発生時間 (ti:i =1~n) における不信頼度 F(ti) を推定し、ワイブル解析では平面座標としてワイブル確率紙(ワイブルチャート)にそれをプロットする。次に全プロット点を代表する直線(回帰直線)を当てはめ、この直線と確率紙で定義されている縦軸と横軸の関係から母数と信頼性特性値(B10など)を推定する方法である。最初に記載した解析条件(試料数と故障数)は、プロット点が分布全域に亘って現れるよう考慮したものである。確率紙以外の特別なツールは必要なくF(ti) を求める式も簡易なため、電卓さえあれば複雑な理論を知らなくても解析可能であり、我々エンジニアにとっては有りがたいツールである。その割にはB10など分布の端の領域を推定する際は、後述する難解な最尤法よりむしろ推定の偏りは小さく適している。
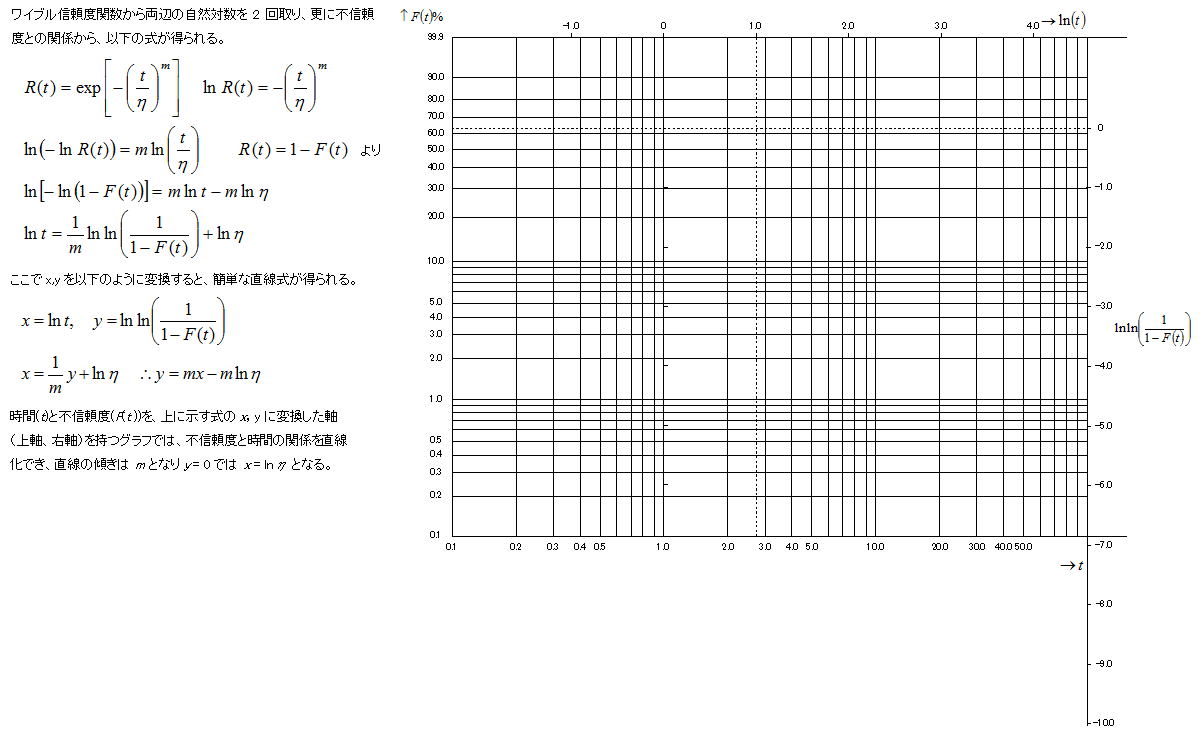
1)ワイブル確率紙(ワイブルチャート)
ワイブル確率紙は、下図のように非直線軸(左軸:F (t)、下軸:t) と直線軸 (上軸:ln t、右軸:ln ln1/1- F(t) ) を持ち、その関係はワイブル信頼度関数から以下のような数理展開で説明できる。
2)不信頼度の計算方法
n個のサンプルサイズで信頼性試験を行い、n個の故障発生時間が観測されたとしよう。つまり完全データでありこれを小さい方から昇順に並べ替えたものを順序統計量といい、この場合の不信頼度を考えてみよう。不信頼度はその時間における故障確率に等しいため、i 番目が故障した際の故障確率は単純にF(ti)=i/nと推定できそうである。管理人も最初はそう思ったがどうやら違うらしい。n が十分に大きくデータの昇順間隔が狭ければ成り立つが、我々が扱う試料数(5~20個程度)では分布の時間領域内に均等に並ぶ可能性が低い(順序統計量ごとのばらつきが大きい)ことがその理由である。データの種類(完全データ、打切りデータ)により幾つかの方法が考案されているが、n個中r番目の故障確率の中央値(メディアン)を推定する考え方が基本となり、これをメディアンランク法といい完全データは元より定時(定数)打切りデータにも適用できる。
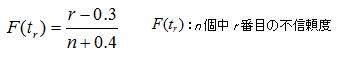
上記以外の方法としては平均ランク法(r/n+1)、モードランク法(r-1/n-1)などがあり、メディアンランク法を含め何れを用いるかは確率分布により一長一短があるが、前記ISO規格ではメディアンランク法で代表できるとしている。ランダム打切りデータでは以下に示すカプランマイヤー法、累積ハザード法の方が推定量の偏りは小さいとされるが、評価者が試験計画段階から関与している場合はランダム打切りデータになる可能性は低く、エンジニアがこの手法を適用することは殆どないと考えてよい。信頼性解析関連の文献では、完全データ、定時・定数打切りデータの解析理論より、寧ろランダム打切りデータの解析理論の方が頁を割いてある傾向にあるが、そもそもランダム打切りデータは母集団を特定することが困難なため、管理人はこの手法を用いて解析した経験は一度もない。参考までに前記ISO規格では中途打切りデータを含む解析例を附属書Bに記載しており、この方法の解析例を下表に示す。先ずデータ順位から逆順位(k)を割り当て、次に平均順位(j)を求めこれを上記の不信頼度を求める式のrに代入し、不信頼度を求めるというものである。管理人のプログラムでは、この方法は累積ハザード法の代替えプログラムとしているが、母数の推定値は累積ハザード法と殆ど変わらないことが確認されている。
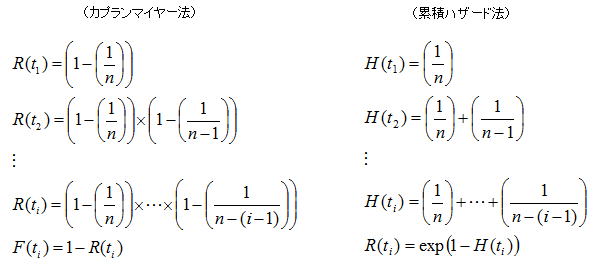

※直前の故障データとは、平均順位の列において値が記載されている直前の行の値をいう。
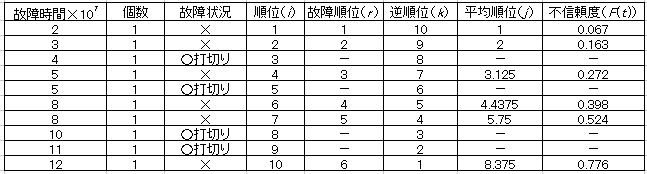
記載データから分かるように、良品打ち切り品を経由した以降の試料の平均順位は通常の故障順位より大きく見積もられており、これに伴い不信頼度の推定値も大きくなる。
3)母数の推定方法

(最小二乗法によるワイブル母数の推定)
二つの変数(ここではln t, lnln (1/1-F(t)))にy = mx-mln ηの関係があると仮定できたとしても、1回の観測でたまたま得られたy の値はx 以外の偶然性による変動の影響により、回帰直線付近には位置するものの直線を中心としてy (不信頼度)及びx (時間)方向にばらつく。 回帰式を導出するための考え方として、x 方向の差(εx)とy 方向の差(εy) の何れを最小にするかで二つの方法があるが、前記した国際規格”空気圧-試験による機器の信頼性評価”ISO19973-1/JIS B8672-1では、x 方向の合計誤差(Σεx)が最小になるように下記式によりmMRR-onX とηMRR-onX を求めるとしている。 信頼限界とはこのばらつき具合の限界のことであり、信頼係数(1-α)に 基づく係数(Kα)により変化する区間を信頼区間という。想定される特性値の下限(最悪)値を見極める手法になる。

4)FM(フィッシャーマトリックス)信頼限界
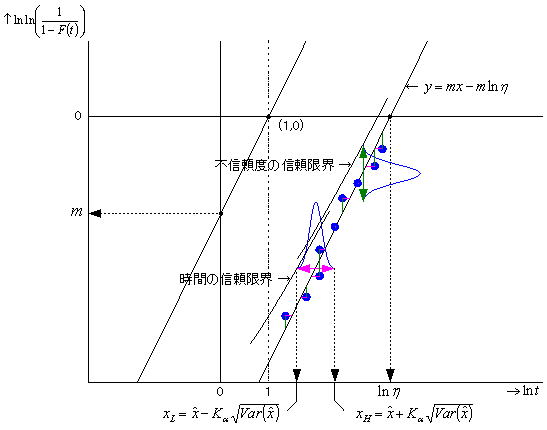
信頼性解析の文献他を漁ると、母数や信頼性特性値の信頼限界を求める幾つかの方法が提案されており、手法により得られる信頼限界の値も微妙に異なっている。ここでは前述の国際規格に記載されている、信頼性特性値の信頼限界を推定する手法(FM信頼限界)について説明する。但し管理人は統計屋でも数学屋でもなく一介のエンジニアであり、文献他に「このように計算すれば求められる」と書かれているので素直にそれをプログラム化し、ツールとして使用しているだけである。FM信頼限界は最尤推定値の分布が正規分布に従う性質を利用し、分散(共分散)の算出に局所フィッシャー情報行列を用いる手法で、理論的な基礎は最尤法にあるといわれている。これには時間と信頼度の二つのタイプがあるが、我々の関心は一定の故障率(不信頼度)に至るまでの時間にあり、殆どの場合は前者(時間)を対象とした信頼限界である。
時間の信頼限界:不信頼度を一定とした場合の時間の信頼限界
信頼度の信頼限界:時間を一定とした場合の信頼度(不信頼度)の信頼限界
この関係をワイブル確率紙の直線軸で表すと下図のように表せる。この関係は統計解析における回帰分析と同様の考え方が適用でき、時間の信頼限界は回帰直線からのX軸(lnt)方向のばらつき、不信頼度の信頼限界はY軸(lnln(1/1-F(t)))方向のばらつき具合に因ることになる。前述のワイブル確率紙における直線式により、信頼度(y:不信頼度)が与えられた際のx の点推定値及びその(1-α)%の信頼限界は以下により求められる。Var(x)を求めるためにはm 及びη の分散及び共分散が知られていなければならないが、この際に局所フィッシャー情報行列が適用される。我々エンジニアにとっては最後の式の論理展開に構っている暇はなく、単にVar(x)を求めるにはどうしたらいいかの一点だけである。

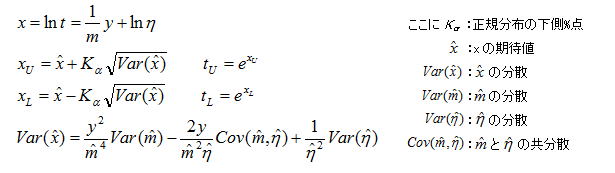
先人の方々の努力によりこれを求める式も既に分かっており、以下の行列式の各要素を計算することで求められるが、この辺りの論理展開も我々にとっては素通りする以外ないが、一般式としてここまで明らかになっているのでツール(EXCEL、専用プログラムなど)を用いて計算すれば、実際数学が苦手の管理人でさえもFM信頼限界を求めることができている。
(局所フィッシャー情報行列による各分散及び共分散の計算方法)


7.2最尤法(MLE)
ワイブル解析で十分な客観的評価が得られるため、管理人を含め”一般的なエンジニア”は難解な最尤法は避けて通りたいところである。しかしかつては仮に理論が理解できたとしても、とても計算して答えが得られる代物ではなかったが、時代が変わってPC上で複雑な数値計算結果があっという間に得られる世の中になり、信頼性解析ツールとしての最尤法の適用は今後拡大することが予測される。実際管理人のプログラムも、最尤法とワイブル(グラフィック)解析結果が同時に得られるようにしているが、形状Par.の偏りを補正した場合の一致性は驚くほどであり、信頼性データと数値計算の組み合わせだけで分布を特定できるのは、非常に素晴らしいことである。但しツールが活用できるとはいえ、我々にとって難解な理論であることには変わりない。未知の母数θ
を持つ母集団の分布をf (x;θ)とし無作為標本から観測された実現値をX1=x1, X2=x2 ,,, Xn=xnとすると、実現値が同時に観測される確率は確率密度の積 f (x1;θ )・f (x2;θ )・・・f (xn;θ )で与えられ、これをθの尤度関数 と呼ぶ。この尤度が最も大きくなる θ を、未知の母数θの推定値とする考え方である。実際の計算にあたっては対数尤度関数が用いられ、θを求めるにはそれを0
と置きその偏微分方程式を解くことになる。ここまでの前置きの一般論は何とかなるが、ワイブル尤度関数に展開しm とη の偏微分方程式を整理する辺りから、管理人だけかも知れないが少し理解が怪しくなる。「理解が怪しいまま進むのは何事か」と叱られるのは承知しているが、最終的には母数を推定する一般式が公開されているので、これを用いることで母数の最尤推定値を求めることは可能である。但し前述したように手計算は到底無理であり、ニュートンラプソン法と呼ばれる反復計算(コンピュータが得意とする収束計算プログラム)を用いる必要がある。
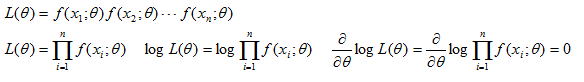
理解を困難にしている一つの理由に文献によりワイブル尤度関数の表現が異なる点があるが、以下の展開式でいいように思われる。先ずm を推定する式ε(m)によりm の最尤推定値をニュートンラプソン法により求め、その値をη を求める式に代入しη を求めることになる。
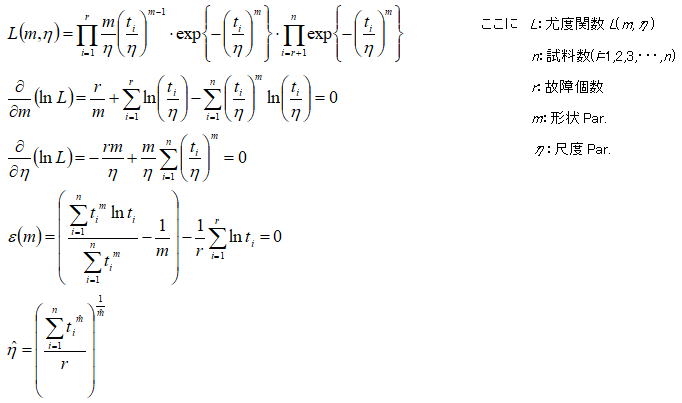
(留意点)
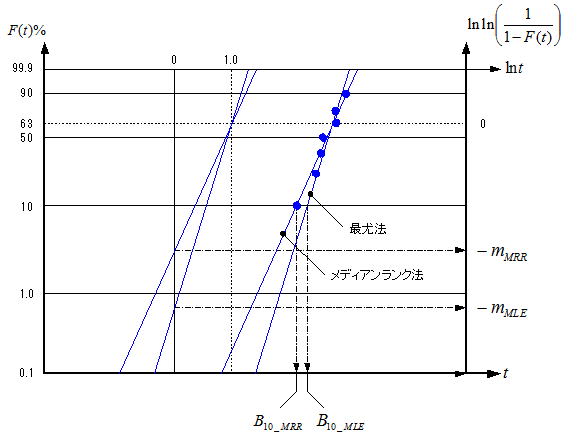
このようにして得られる最尤推定値であるが、残念ながら我々エンジニアが扱う試料数(5~20個程度)では形状Par.(m)の値に偏りがあり、特に試料数が10個以下の場合はこの影響が大きい。この偏りは試料数と母集団の分散(つまりm の値)により変化するが、管理人の経験からは概ね最尤推定値の方がワイブル解析(メディアンランク回帰法)より大きくなる。下図に示すように平均値(F(t):50~60%)付近では殆ど差はないが、分布の両端付近では差が大きくなる傾向がある。但しここでは公開できないが形状Par.の偏りを補正する係数(試料数により変化する補正係数で、試料数が少ないほど補正量は大きい)が発表されており、これを考慮すると驚くほどワイブル解析結果と一致することが、管理人のプログラムでも確認されている。従って最尤推定値で信頼性特性値(特にB10など不信頼度が小さい領域)を推定する際は、この偏り(分布の両端の方が影響が大きくなる)を念頭に置く必要がある。もう一つの留意点として、データさえあれば数値計算としての解は得られるが、それらをワイブル解析した際の直線への当てはめ性までは判断がつかない。つまり2項のような層別を必要とするデータであっても一つの分布として解析してしまう可能性があるため、最尤法のみで結論を得る(解析する)ことは避けるべきである。
7.3故障数が0個の場合の推定方法
単純に考えると、「故障数が0個の場合に母集団の分布を特定できるのか」という疑問が湧いて当然であるが、理論はこのような場合でも助け舟を出してくれるので有難い。エンジニアには時間もコストも潤沢に与えられていないため、実践面ではむしろこの理論を適用するケースの方が多いのではないだろうか。実際管理人も多くのケースでこの理論を適用してきたが、顧客へ信頼性データを提供する場合を含め、信頼性を客観的に評価する観点からも十分有効な手法といえる。
1)ワイブル分布と仮定(二項分布法による信頼度の推定)
故障数が0個の場合は7.1項のように不信頼度を求めることができないため、メディアンランク回帰法などによる分布の特定はできない。ここでは故障分布をワイブル分布と仮定した上で、形状Par.が過去の同類のライフデータ、または技術的な判断から既知とした場合の推定方法を説明する。コイン投げ(確率1/2)や、さいころの目の出方(確率1/6)など1回の試行で生じる確率をp としてその試行をn 回繰り返した際に、特定の事象が発生する回数は二項分布に従うことが知られている。二項分布は信頼性解析とは少し隔たりがあるように感じられるが、パラメータp を時間的な要素に置き換えることで、信頼性モデルとして扱うことが可能になる。すなわちn 個の試料数で信頼性試験を実施し、ある時間t まで試験を継続した際の生存(若しくは故障)数と考えれば置き換え可能(二項分布と仮定できる)で、更に具体的には試料数n、試験終了時点の故障数をy、個々の試験ユニットの故障確率をp とすると、故障がy 個発生する確率p (y)は二項分布の確率関数より以下の式で求められる。本項の関心事である故障数が0個となる確率p (0)は、以下に示すように(1-p)nになる。

上の考え方は確率問題であり時間的な要素は一切含まれていないため、信頼性モデルへの置き換えをもう少し進めてみよう。同じ信頼度(若しくは不信頼度)を有するn 個の機器を信頼性試験に投入し、ある時間ti まで動作させた際の故障数がy 個になる確率と考えれば良さそうである。この場合のパラメータp は不信頼度F (t)に相当し、信頼度との関係からn 個の試料数において故障がc 個発生する確率pg(y)は以下のように展開でき、更に故障数が0個(y =0)となる確率pg(0)はR(ti)n となる。
この展開式における関心事は、ある時間ti における信頼度R(ti) ということになるが、この値を推定する際は信頼区間の下限値(信頼度は上限より下限の方が厳しい評価になる)を推定する必要があり、それは片側信頼水準(Pα)を設定しpg(y)=1-Pαと置くことで求められる。このように書くといきなり「片側信頼水準」という言葉が出てくるので若干の違和感があるが、そんなに難しいことを言っている訳ではない。単純にはある時間ti まで試験した際に、故障がc 個(0,1,2,・・・)発生する確率がある値(1-Pα)より大きいか小さいかの問い掛けであり、この設定値により信頼度が変わるため、故障数に応じてそれを推定しようというものである。大きいか小さいかの問い掛けとは、具体的には信頼性試験が成功に導かれるか否やの判断であり、評価者としては片側信頼水準の値を大きくしたい(β=1-Pαと置くとβは小さくしたい)ところではあるが、これに応じて見合う信頼度は小さく見積もられるので、試験を成功に導くには厳しい評価となる。なおβを消費者危険率といい、顧客にとってはこの値が小さい程信頼性の評価ポイントは高くなる。
前述のISO規格ではこの考え方を次のように説明している。「n 個の機器をある時間ti まで試験した際に1個以上が故障する確率は最大に見積もっても(1-R(ti)n)であるが、この値が1に近いある確率Pα(0.99,0.95,0.9.・・・)より更に大きいとする仮説1-R(ti)n≧Pαを設け、試験が成功(y =0)に至った場合を考える。すなわちR(ti)nの値が1-Pαより更に小さいとの仮説が否定されたことになり、結果としてR(ti)n ≧1-Pαと考えることができる」としている。以上の考え方よりある時間ti まで動作させた際の故障数が0個の場合の信頼度R (ti)は、1に近いある確率として与えられる片側信頼水準Pα及び試料数n により一義的に決定され、これにワイブル信頼度関数を代入することで最後の式が得られる。式より信頼度は、試料数を一定とすると片側信頼水準を大きくする程小さくなり、又片側信頼水準を一定とすると試料数が多い程大きくなる(8項の計算式において最短試験規模が短くなる)関係にあり、矛盾点は見当たらない。

上の式は分布のばらつきが分かっている(形状Par.既知) ワイブル確率密度関数f (t) において、一定時間経過後の故障数が0個の場合の信頼度は、試料数と片側信頼水準Pα(若しくは消費者危険率:1-Pα=β)により一義的に決まることを意味している。つまりその時点(ti )で打ち切ったとすると、その時の信頼度R(ti)が推定可能なことを意味している。最後の式において形状Par.を既知とすると未知数はηのみなのでこれについて解けば分布を特定することができ、更に確率計算により信頼性特性値(B10 ,MTTFなど)を求めることができる。信頼性試験においては十分な試験時間がない場合が往々にしてあり、故障数0個で打ち切られる試験も多い。このようなデータから信頼性特性値を得たいとの機会も多く、我々エンジニアにとっては非常に有効なツールとなる。信頼性を評価をする上で、「形状Par.を既知とするような論理展開で大丈夫か」と思われるかもしれないが、同類の機器で何回かの完全データが揃っていれば殆ど問題なく推定することはできる。但しその値はあくまで打切り時間まで故障しなかった証しとしての理論推定値であり、実力値より多少控えめな値になるのは否めない。上の式でy=1,y=2,…y=cと置くと、故障数が1,2,…個における打切り時間の信頼度も推定可能となるが、この場合の信頼度は一義的には決まらず数値計算により求める必要がある。ワイブル分布の計数1回抜き取りLTFR(Lot
Tolerance Failure Rate)方式の合格判定故障個数における信頼度の考え方は、正しくこの理論からの展開である。
2)指数分布と仮定(ソーンダイク芳賀曲線による故障率の推定)
指数分布はワイブル分布においてm =1としたときの分布で、半導体デバイスの寿命分布はこの分布に近似できることが知られている。一方機械構成機器は、バスタブ曲線の三つ(初期,偶発,摩耗)の故障型の混合分布(に従っている)と考えることができる。ここで観点を変えて摩耗型がないとした場合、通常初期型は異常値(10項を参照)として寿命解析から外されるので、偶発型故障のみで解析できることになる。この例としてどのような場合が想定されるであろうか。
故障数がゼロの場合のもう一つの考え方として、打ち切った時間がバスタブ曲線の安定期間内にあると仮定すれば、その機器の故障率は試験経過時間に関係なく一定であると考えることができる。従ってこの期間の寿命分布は指数分布と仮定でき、上の想定される状況と一致する。実際複数個のコンポーネントで構成される修理系の故障時間間隔の分布は、寿命分布の形に制約されず指数分布に近似されることが知られている。指数分布と仮定されるなら以下のような論理展開から特性値(MTTF)を推定できる。
(MTTFの推定方法)
危険率(α=0.1:信頼水準90%)の故障率(λ)の信頼上限:λu
試料数:n
総試験時間:T = n×試験時間(t)

前述の「ワイブル分布と仮定」の推定値が辛めの推定値になるのに対し、この方法ではかなり甘めの推定値になるため管理人はこの方法を用いたことはない。この方法においては、試験打切り時間以降も仮定が成り立つ(つまり同一の故障率が維持継続)ことが前提であり、これを担保するには結局更なる試験時間が必要となり実用性に乏しい。
7.4他の推定方法
信頼性データの取得には大きな二つの壁があり、折角多くの時間を掛けて試験を実施したのにデータ解析を中途半端にすることは大きな損失であり、評価者としては解析における推定量の偏りや分散は出来るだけ小さくしたいところである。推定量の確かさの尺度として平均二乗誤差(MSE:mean
square error)というものがあり、文献にはこの値をできるだけ小さくする推定(パラメータの)方法が幾つか挙げられている。故障分布が2母数ワイブル分布と仮定できる場合、先ずやるべきことはワイブル確率紙によるメディアンランク回帰、次いで最小二乗法による母数の推定になるが、これ以外にも幾つもの手法が考案されており、手法により母数の推定量のMSEは微妙に異なっている。これらの手法としてはワイブル分布から変換させた二重指数分布を用いたモーメント法(MME,MNE)、線形推定法(BLUE)、最小二乗法(Gumbel)などが考案されているが、これらの推定方法は信頼性解析というより数値解析の範疇であり、管理人を含め"一般的な"エンジニアが製品の開発プロセスでこれらの方法を用いて推定することには限界があろう。管理人の実践経験では、7.1~7.3項における推定方法で推定量の不適合を経験したことはないが、閲覧者諸兄において本サイトに記載されている推定方法を実践された上で、更に高度な推定方法を試みようと思われた方は是非チャレンジして頂きたいと思う。
8.最短試験規模
信頼性試験を実施するにあたっては、7.1,7.2項の考え方によりその製品の実力値を得たいと誰もが思うところである。しかし信頼性試験における二つの壁(数と時間)が立ちはだかり、その全てで実力値を得ることは至難の業である。前述の国際規格でも、設計原理が同じシリーズ(つまり機能設計が同一母集団として代表できる)では、全ての型式又はサイズで試験する必要はないとしており、代表できる実力値が得られている場合はその製品の目標値さえ宣言できれば十分であり且つ合理的である。実力値は分らないまでも試験時間を短縮する方法として予め
B10の目標値を設定しておき、それを一定の信頼水準(あるいは危険率)で宣言できるまで試験を継続し、故障数0個で打切りとする考え方がある。この時間を最短試験規模といい、二つの壁を克服する手法の一つでありエンジニアにとって非常にありがたいツールとなる。故障分布がワイブル分布と仮定でき過去の試験によりその形状Par.が既知である場合の方法を説明する。Bp の目標値を tp 、Bp 時の信頼度をR (tp) とすると、ワイブル信頼度関数から以下のように展開できる。
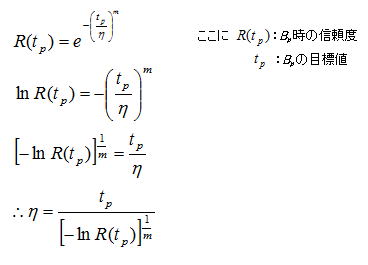
次に7.3で示した故障数ゼロにおける信頼度の式に着目し、最短試験規模 ts、試料数n 、片側信頼水準Pα とすると以下のように展開できる。

以上の展開式にワイブル信頼度関数からのη を代入し整理すると、最短試験規模(ts)と目標値(tp) の比を求めるための下記式が得られる。この式は何れを未知数とするかで幾つかの対応が可能で、非常に利便性が高い展開式である。ここまでの論理は目標値と片側信頼水準(Pα)を与え、目標値を宣言できるための最短試験規模を求める展開であるが、未知数を逆にすれば試験時間から宣言できる目標値も推定可能である。次に最短試験規模と目標値を与え未知数をA として計算すれば、片側信頼水準から危険率(β:9項を参照)を求めることも可能となる。更にもう一つの展開として、この式の信頼度(R (ts))は故障数 c = 0 を前提としているが、故障個数に応じた信頼度 を与えることができれば、 c ≠ 0 の場合にも適用できる。但し c ≠ 0 場合の信頼度は、c = 0 の信頼度が一義的に決定されるのに対して少し計算が複雑となり、9項により求める必要がある。摩耗系故障を扱う場合の一般的な目標値はB10ライフ(R(tp)=0.9)、片側信頼水準90%((1-Pα )=0.1)になるのでA ≒21.9となる。

9.ワイブル分布の計数1回抜き取りLTFR(Lot Tolerance Failure Rate)方式
既に知られているように統計的品質管理(SQC)における抜き取り検査は、ロット(母集団)から抜き取られた大きさn の不良個数などによりロットの合否判定を行う手法である。信頼性の場合の抜き取り検査では、不良率(p)の代わりに故障率(λ)が導入される。信頼性の抜き取り検査では指数分布を仮定する場合が一般的であるが、解析アイテムが摩耗系故障の場合は指数分布は必ずしも適切ではない。摩耗系故障に適用できる抜き取り検査としては、「ワイブル分布の計数1回抜取LTFR(Lot Tolerance Failure Rate)方式」が適している。
形状Par.(m )を既知として試料数(n )、合格判定故障個数(c )、消費者危険率(β)が与えられたとき、試験時間ti までに故障がc 個発生する確率pg (y)は以下の式で表される。故障個数が0個の場合の左辺はR(ti)n となる訳であるが、7.3項では片側信頼水準Pαを与え確率値として(1-Pα)と比較している点が異なる。但し前述したように(1-Pα)=βの関係にあるため、結局比較する確率値は変わらないことになる。この式において未知数である信頼度(R(ti))を求め、8項の最短試験規模(ts)と目標値(tp)の比を求めるための式における(R (ts))を置き換えれば、故障個数が1個以上ある場合でも8項の考え方が適用可能となる。つまり目標値(tp)であることを宣言できる時間(ts)まで試験を継続し、故障個数0個で試験を打ち切る考え方が最短試験規模で、一方LTFRは試験時間(ti )までの故障個数が0個(必ずしも0個とする必要はない)であるなら、目標値(tp)を満足(合格)と判断する訳である。なお故障個数が0個の場合の信頼度は7.3項の式により手計算で簡単に求められるが、c ≧1 の信頼度は手計算で求めることは困難なためプログラムによる数値計算により求める必要があり、下表に計算結果(β=10%)の例を示す。各故障個数における信頼度は、片側信頼水準(若しくは消費者危険率)を一定とすると試料数が多い程大きくなっており、これに伴い最短試験規模は短くなる。
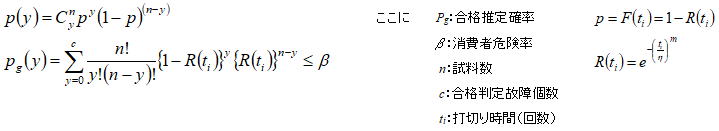
10.異常値の判断
信頼性データを取得後に順位統計量として整理する際に、頻度としては稀ではあるが取得したデータの中に異常値ではないかと疑われる場合がある。ここではそれを異常値として解析対象から除外すべきかの判断方法を示す。特に試作(量産試作を含む)段階では、初期的な偶発故障が発生する可能性があるため注意したい。何れにしてもそのデータを母集団に含めるや否やは評価者の感性ではなく、客観的な判断で行う必要がある。異常値と疑われるようなデータが確認されたら、先ず全データの平均値(μs)と標準偏差(σs)を推定し、平均値からの隔たりを規準化(ui=(xi-μs)/σs)する。次に異常値と疑われるデータ(ui が最も大きい)を外した平均値と標準偏差を再計算し、外したデータを含めた全データのui を再計算する。つまり平均値から著しく離れたデータの有無を確認する訳であるが、最終的には発生確率で判断することになるため全データの発生確率(pi:t 分布の両側確率)を推定する。
異常値が発生する確率をp とすると異常値が含まれない確率は(1-p)なので、信頼性試験に投入したn 個の試料数で異常値が全く含まれない確率は(1-p)n と計算される。これより逆に異常値が含まれる(1個以上)確率(Px)は、Px=1-(1-p)n になる。この値をある基準に設定し、異常値と疑わしいデータの発生確率(pi)を代入してPxを求め、基準値に対して大きい(通常起こり得る→解析データに含める)か小さい(起こり得ない→解析データから除外する)かで判断する。前記ISO規格ではPx=5%で判断するとしている。
11.実践にあたって
以上述べてきた範囲で機械構成機器の摩耗系故障における解析は十分実施できる。これにFMEA手法と電子機器の信頼度予測法を手にすれば、エンジニアにおける信頼性解析レベルはほぼ満たされるが、多忙な開発業務の中でこれらに精通できるかといえばなかなか厳しい状況ではある。エンジニアは自分が設計した製品の信頼性を、設計審査において定量的客観的に示す必要があるが、信頼性解析では二つの壁があるため何とかこれを克服する必要がある。この観点から状況に応じた手法の選択が重要である。
1)実力値を評価したい場合
7.1,7.2項の方法により解析することになる。試料数はn≧7個が望ましい(最初の不信頼度のプロット点が10%を下回るため)が、7個以上製作が困難な状況はいつでもあり厳格に拘る必要はない。但し故障数に関しては試験投入数の70%以上が故障することが望ましく、特に試料数が少ない場合(n≦6)場合は完全データ(全数故障)が望まれる。なお実力値を評価する場合でも、一連の故障が予測された故障モードであるなら、7.3項の考え方などにより信頼性特性値(B10,MTTFなど)を試験の中間点(故障数:0,1,2,…)で推定することも可能である。管理人は中間報告などで適宜この方法を用いて評価したが、その推定値が最終的な結果と大幅に外れたことは殆どない。従って信頼性試験を実施する際は、同類の信頼性試験における形状Par.を保有しているかが結構重要なポイントになる。
2)目標値であることを宣言したい場合
8項に従って最短試験規模を設定し、その時間(回数)に達したら故障数0個で試験を打切る。この方法では真の実力値は分からないまでも、試験の短縮が可能になる点が大きい。試験時間は試料数(n)で大きく変わるので、可能な限り試料数は多く取った方がよい。なおワイブル形状Par.は過去の同類の試験などにより解析値がある場合はそれを採用し、無い場合は予測範囲内で小さい値を見積もっておけば、顧客に対する影響(消費者危険率)を小さくできる。
(一般的な推定条件の例)
信頼性特性値:B10
消費者危険率:10%
故障個数:0個
ワイブル形状パラメータ:機械構成機器の摩耗系故障における参考値(m ≧4~6)
3)加速試験について
加速信頼性試験は一つの壁(時間)を切り崩す有効な手法とされ、信頼性解析に関するどのような文献にも殆ど触れてあり、最近ではステップストレス試験など新しい考え方の理論も公開されている。しかしいざ実践しようとするとこれがなかなか困難である。JIS
Z8115によれば「試験時間を短縮する目的で、基準より厳しい条件で行う試験で、故障モード及び原因が変わらないことが必要」と規定されている。更にもう一つ、加速時に故障分布の分散(ワイブル分布では形状Par,値)が変化しないことが重要で、これが実践する上で大きなネックポイントになる。
これらの関係をワイブルチャートと確率密度関数で表すと下図のようになる。すなわち分布の分散はほぼ同じままで、分布の位置(ワイブル尺度Par.:η)が時間軸の小さい側に(ηa=ηn/Ak)変わるため、見掛け上寿命が短くなる訳である。単に加速させるだけなら、環境条件、使用条件、設計パラメータの変更、故障基準の厳しさなどの因子水準を、故障モードが変わらない範囲でストレス分布の厳しい側(加速方向)にシフトさせれば加速されるので、試験を実施すること自体の困難性は大きくない。問題は得られた信頼性データの扱い方と、試験の再現性(異なるラボ、異なる評価者が同じ条件で実施して同様な結果が得られる)である。
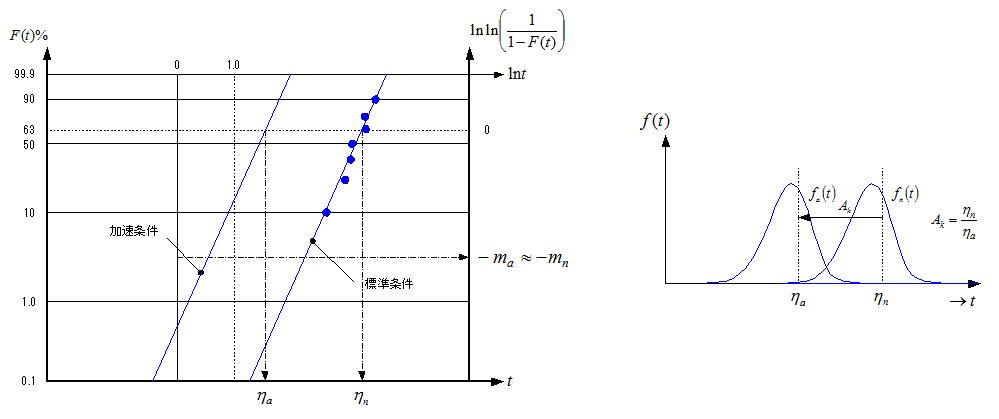
一番のポイントは加速条件で得られた信頼性特性値が、標準条件においてその値×加速係数として担保できるかであろう。仮に設定した加速条件で標準状態に比較しAk=5.0が得られたとしよう。次に同類の別の製品を加速試験に投入しB10aが得られたものとする。この結果から標準条件におけるB10nをB10n=B10a×Akとして担保できるかである。一見すると問題なくできそうであるが、形状Par.が平行移動するかというとこれがなかなか思うようにコントロールできないことが多く、更に同類(同一シリーズ)製品であっても加速係数が多少異なる場合もあり、理論と実践は単純には折り合わないようである。加速試験における形状Par.の変化(分散の変化)は、故障モードが想定される範囲か否やつまり通常の摩耗系故障の範囲に留まっているかが重要で、大幅に変化した場合は破損・欠損など全く別の故障モードになっている可能性が高く、加速因子の水準を見直す必要がある。これは加速条件の母集団の範囲(試験条件と製品の範囲)を特定することが、かなり困難であることを意味している。言い換えると一つの製品シリーズであっても、一つの加速条件(母集団の範囲)では成り立たず、一律の加速係数を得るには加速条件を幾つか設定する必要があると思われる。勿論管理人は加速寿命試験を否定している訳ではなく、時間を切り崩すための有効な手法であるとの認識には変わりない。
4)ツールの解析結果に対する留意点
7.2項の(留意点)にも書いたが、ツールを使用して解析する場合は注意が必要である。特にワイブル解析(メディアンランク回帰法)では、解析ツールはどのようなプロット点の配置であっても、最小二乗法により自動的に回帰直線が引かれその直線により母数が推定される。プロット点の配置チェックでは幾つかの留意点があるが、最も注意しなければならない点は二つ以上の母集団が混合している混合型ワイブル分布の有無である。本来これらは層別する必要があるが、誤解を恐れずにいえば評価者のさじ加減でどうにでもなる可能性があり、特に市場データを扱う際は顧客の設備使用条件など、母集団の範囲を特定できる情報が必須となる。