

1.概要
冒頭から否定的な見解で申し訳ないが、開発プロセスにおいてエンジニアが実験の試料数を設計できるなら何の苦労も要らない。近年開発コストは非常にシビアに設定されるため、試作品を評価する為のサンプルサイズ(以降試料数ともいう)は、その製品の開発予算の枠内で何個製作できるかで決まることが多く、評価者(開発担当者)が試料数を設計できる自由度は殆どないと言っていい。教科書通り(特にばらつきを見極めるための試料数)に製作していたのでは開発費がいくらあっても足りないので、正直管理人も実験計画法に基づく割り付け実験以外では、試料数を予め設計して実験を行った経験は少ない。但し事前設計が仮にできないとしても、実験を実施した後の統計的判断(結果)を評価する際に、その結果における試料数と検出力の関係は明確にしておきたいところではある。本編はこの為に記載したものであるが、勿論事前に試料数が設計できればそれに越したことはない。
2.サンプルサイズ
仮説検定と推定のページでも述べてあるように、何れの解析結果においても試料数が重要な鍵を握っていることが分かる。例えば仮説検定では試料数が多いと小さい差又は比を「第二種の誤り」の確率(β)が小さい条件、若しくは検出力(1-β)が高い条件で検出(判断)できる。前述したようにエンジニアは試料数を設計できる自由度は低いが、仮説の設定内容(評価者が知りたい情報)に見合う試料数であることが望ましい。サンプルサイズの設計とは、評価者が知りたい情報を元に予め試料数を実験の計画段階で決定しておくことをいい、検定の種類に応じて設計することになるが、ここでは我々エンジニアが工程能力を評価する際に最も使うであろう以下の条件(一つの母平均の片側検定、一つの母分散の片側検定)について検討する。
2.1一つの母平均の片側検定(H1:μ>μ0又はμ<μ0)・母分散未知
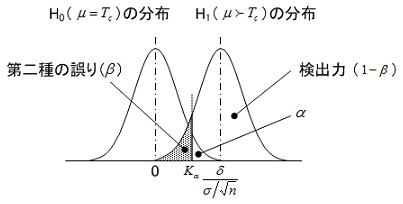
分かりやすくするため、母分散が既知の場合の母平均が目標値(Tc)であるかを片側検定する際の、検定統計量![]() のH0とH1における分布を考えてみよう。u は下図に示すようにH0のもとではN(0,1)、H1では(
のH0とH1における分布を考えてみよう。u は下図に示すようにH0のもとではN(0,1)、H1では(![]() ,1)に従うことが知られている。片側検定(α=5%)であること及び
,1)に従うことが知られている。片側検定(α=5%)であること及び![]() においてβ=10%(言い換えると検出力1-β=90%)の条件を適用すると、以下のような関係式が得られる。すなわちσは既知なのでδのσ倍率により試料数は決まり、δが小さくなる(小さい差を検出したい)と試料数は大きくなることが分かる。
においてβ=10%(言い換えると検出力1-β=90%)の条件を適用すると、以下のような関係式が得られる。すなわちσは既知なのでδのσ倍率により試料数は決まり、δが小さくなる(小さい差を検出したい)と試料数は大きくなることが分かる。

母標準偏差が分かっている場合は以上の通りであるが、一般的には母分散が既知である場合は殆どなく未知であることが多い。母分散が分かっている場合の式![]() は、未知の母標準偏差を含んでいるのでこのままでは分布は特定できない。そこで試料統計量の分散から求められる
は、未知の母標準偏差を含んでいるのでこのままでは分布は特定できない。そこで試料統計量の分散から求められる![]() をσの推定値として代入すると、以下の式で示す統計量が得られる。
をσの推定値として代入すると、以下の式で示す統計量が得られる。
![]()
このような推定値を含む統計量は正規分布には従わず、この統計量はH0のもとでは自由度φ=n -1のt分布に従う。ここまでの論理展開は特に問題ないが、ではH1における分布はどのような分布に従うのであろうか。母分散が既知におけるu の分布はH1のもとでは上図のように単に定数分平行移動するだけであるが、母分散が未知の場合のt は少し違うようである。我々は統計屋になることが目的ではないのでこの辺りの理論を詳細に知っておく必要はないが、この分布は我々にはあまり馴染みがない自由度φ=n -1非心度![]() の非心t分布に従い、δが大きくなるとtよりばらつきが大きくなる。非心t分布の密度関数はかなり複雑で計算が厄介なため幾つかの近似法が考案されており、片側検定におけるサンプルサイズは以下の式で求められる。
の非心t分布に従い、δが大きくなるとtよりばらつきが大きくなる。非心t分布の密度関数はかなり複雑で計算が厄介なため幾つかの近似法が考案されており、片側検定におけるサンプルサイズは以下の式で求められる。
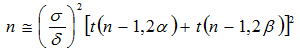
2.2一つの母分散の片側検定(H1:σ2<σ02)
基本統計量の一つである偏差平方和S は、分散の源になる値でばらつき具合を表す統計量である。母分散がσ2の母集団から抜き取られたn 個のサンプルから求められた平方和S をσ2で割った統計量![]() は、自由度φ=n -1のχ2分布に従うことが知られており、母分散に関する仮説検定と推定はこの分布を利用して行うことができる。例えば工程能力Cp>1.0を検定する場合は以下のような仮説条件になる。
は、自由度φ=n -1のχ2分布に従うことが知られており、母分散に関する仮説検定と推定はこの分布を利用して行うことができる。例えば工程能力Cp>1.0を検定する場合は以下のような仮説条件になる。
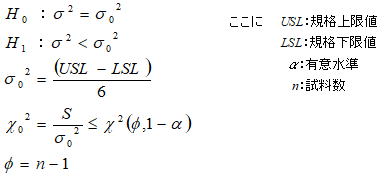
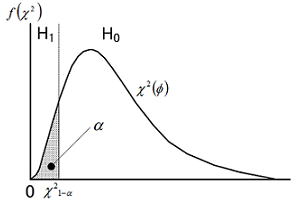
u の分布と同様に、サンプルサイズ(n)と分布確率(α又は1-β)を関連付けることはできないだろうか。H0におけるαは検定比![]() を用いて以下のように定義できる。サンプルサイズはχ2分布の自由度として入っているためこのままではn を求めることはできないが、Δを任意値として決定すれば未知数はn のみであり、収束計算プログラムにより求めることはできる。直接n を求めるための論理展開は少し難解であるが、参考文献によれば以下最後の式で近似できるとしており、SA&RA ProXではこの式を用いて計算している。
を用いて以下のように定義できる。サンプルサイズはχ2分布の自由度として入っているためこのままではn を求めることはできないが、Δを任意値として決定すれば未知数はn のみであり、収束計算プログラムにより求めることはできる。直接n を求めるための論理展開は少し難解であるが、参考文献によれば以下最後の式で近似できるとしており、SA&RA ProXではこの式を用いて計算している。
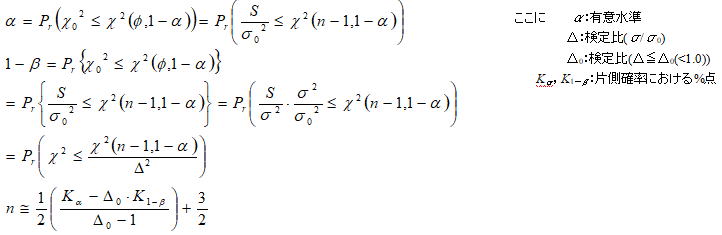
3.検出力
仮説検定においては影響の大きい第二種の誤り(β)、つまり本当は帰無仮説が正しくない(H1の分布)のにH0を棄却しない誤りをできる限り小さくすることが肝要である。言い換えると検出力1-βをできるだけ大きくすると、H0の採択又は棄却に関わらず都合がいいことになる。しかし所要の分解能(検定差、若しくは検定比)を確保した上で、検出力を上げるための評価者側の手立てはサンプルサイズ(~を大きくする)以外になく、その設計自由度が低いエンジニアにとっては低い障壁ではない。
3.1一つの母平均の片側検定(H1:μ>μ0又はμ<μ0)・母分散既知/未知
2.1項同様に母分散既知における検定統計量(u)と、各検定条件における有意水準の関係を考える。2.1項の図において、H0におけるαは検定統計量(u)が従う分布より以下のように定義される。H1における検出力1-βは以下の式により求められる。
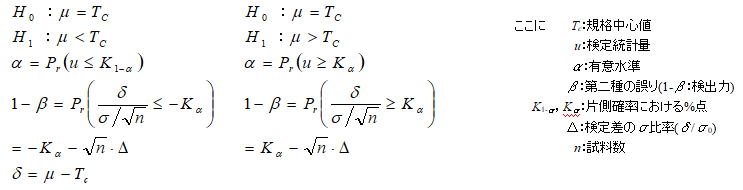
母平均の片側検定同様に母分散が未知の場合の統計量![]() は、H0のもとでは自由度φ=n -1のt分布に従うためH0におけるαは以下のように定義される。H1における検出力1-βは以下の式により求められるが、H1のもとではt0は非心t分布に従うためこの計算が必要であるが、これを求めるための近似式が示されているのでこれを用いて計算する。
は、H0のもとでは自由度φ=n -1のt分布に従うためH0におけるαは以下のように定義される。H1における検出力1-βは以下の式により求められるが、H1のもとではt0は非心t分布に従うためこの計算が必要であるが、これを求めるための近似式が示されているのでこれを用いて計算する。
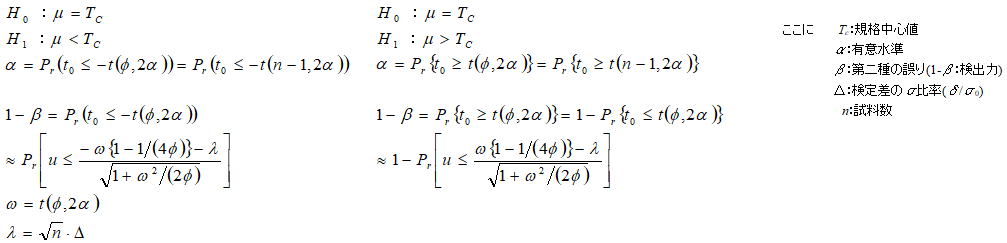
3.2一つの母分散の片側検定
H0における有意水準(α)は、検定統計量(S/σ02)が従う分布より以下のように定義される。
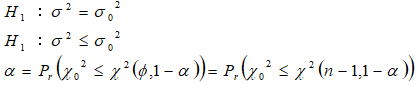
検出力1-βは以下のように計算できる。
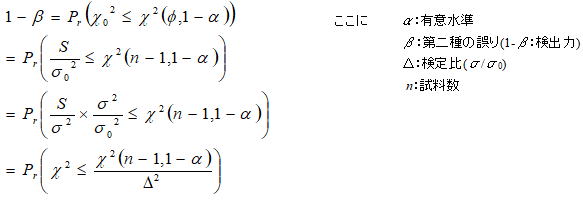
4.検出力と試料数の関係
4.1検定差(又は検定比)と試料数の関係
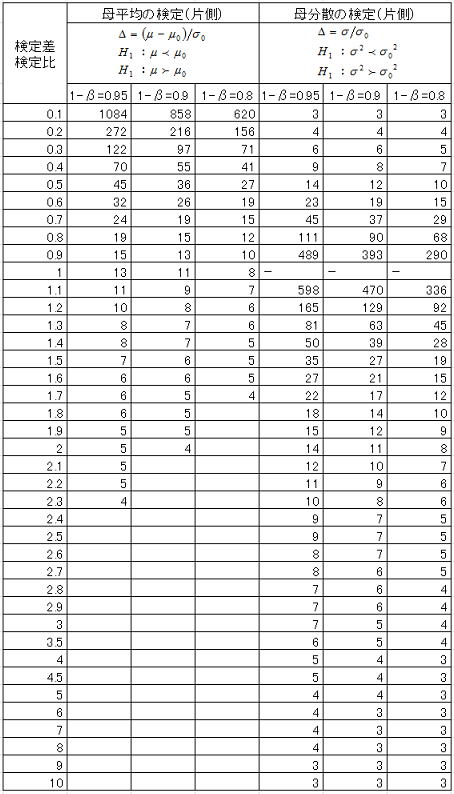
所要の検定差(比)において一定の検出力を得るための試料数(SA&RA ProXによる計算結果)を以下に示す。我々エンジニアが常用する試料数の範囲(5~20個程度)では、母平均の検定では検定差として1σ程度の分解能(十分とは言えないが一応の許容範囲)があるが、母分散の検定における検定比(![]() ≒1.0が最良)は2倍以上(若しくは0.5以下)の分解能であり、ばらつきを精度よく検証するには明らかに不足である。管理人の経験からは工程能力を評価するための検定比は1.0~1.3倍(若しくは0.7~1.0)、試料数としては50個以上が一応の目安となる。
≒1.0が最良)は2倍以上(若しくは0.5以下)の分解能であり、ばらつきを精度よく検証するには明らかに不足である。管理人の経験からは工程能力を評価するための検定比は1.0~1.3倍(若しくは0.7~1.0)、試料数としては50個以上が一応の目安となる。
4.2試料数と検出力の関係
1)母平均の検定
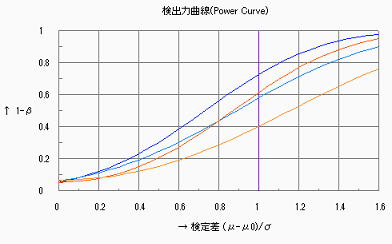
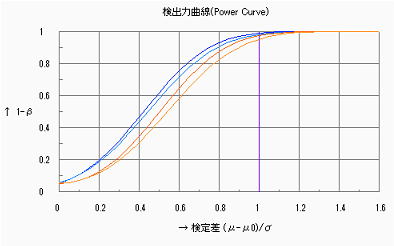
検定差⊿=![]() を検定する場合の、各試料数(n=5,n=10,n=15)における検出力の変化(SA&RA ProXによる検出力曲線)を下図に示す。グラフは
を検定する場合の、各試料数(n=5,n=10,n=15)における検出力の変化(SA&RA ProXによる検出力曲線)を下図に示す。グラフは![]() のものであるが、
のものであるが、![]() の領域は検定差0の軸で対象になる。同じ検定差(例えば
の領域は検定差0の軸で対象になる。同じ検定差(例えば![]() =1)では試料数が増大すると大きくなり、同じ試料数では検定差が小さくなる(検定の分解能を上げる)と検出力は小さくなる。グラフから分かるようにn=5では
=1)では試料数が増大すると大きくなり、同じ試料数では検定差が小さくなる(検定の分解能を上げる)と検出力は小さくなる。グラフから分かるようにn=5では![]() =1でも0.8を下回っており、母平均の検定ではn≧10は確保したいところである。
=1でも0.8を下回っており、母平均の検定ではn≧10は確保したいところである。
n=5 n=10 n=15
2)母分散の検定
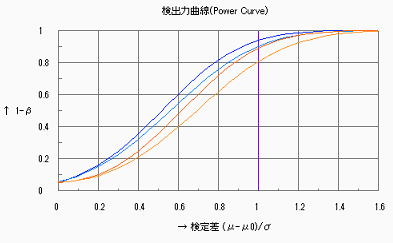
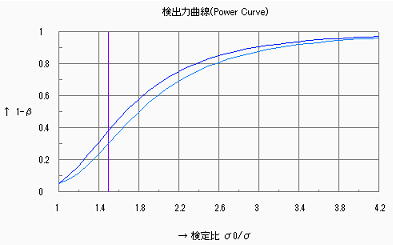
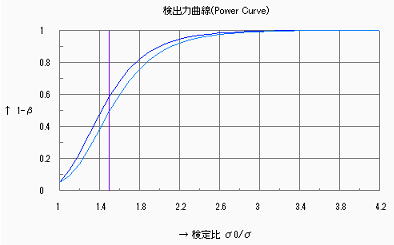
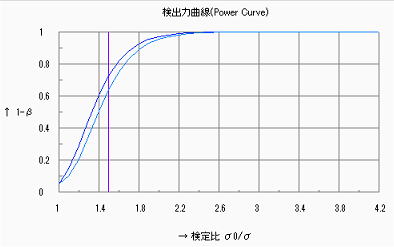
検定比⊿=![]() を検定する場合の、各試料数(n=5,n=10,n=15)における検出力の変化(SA&RA ProXによる検出力曲線)を下図に示す。グラフは
を検定する場合の、各試料数(n=5,n=10,n=15)における検出力の変化(SA&RA ProXによる検出力曲線)を下図に示す。グラフは![]() のものであるが、
のものであるが、![]() の領域は0.5以下で急速に1.0に漸近する。同じ検定比(例えば
の領域は0.5以下で急速に1.0に漸近する。同じ検定比(例えば![]() =1.5)における試料数の増減、同じ試料数における検定比の大小に対する検出力の変化は母平均と同様である。母分散の検定ではn=15でも0.8に至る検定比は1.5以上であり、我々が扱う試料数範囲では分散を検定するには不足であることが分かる。
=1.5)における試料数の増減、同じ試料数における検定比の大小に対する検出力の変化は母平均と同様である。母分散の検定ではn=15でも0.8に至る検定比は1.5以上であり、我々が扱う試料数範囲では分散を検定するには不足であることが分かる。
n=5 n=10 n=15
5.実践例
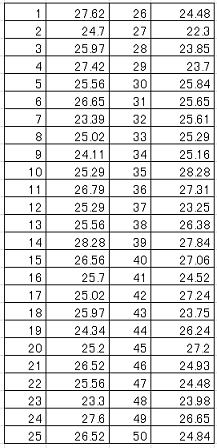
以下のサンプルは仮説検定と推定(実践編)で用いたデータ(n=50)であるが、検出力がどの程度あるかをSA&RA ProXで検証してみよう。
1)母平均の検定
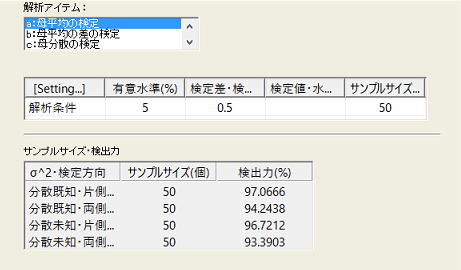
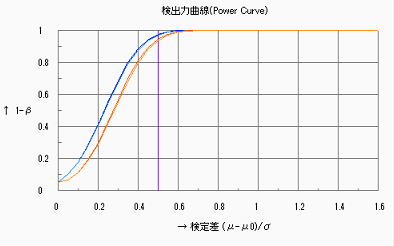
以下に示すように検定差![]() =0.5でも分散未知・片側で96%の検出力があり、工程能力の正確さ(つまりCpkにおける目標値からの偏移量(K)の検定)を見るには、一応十分な試料数と判断できる。
=0.5でも分散未知・片側で96%の検出力があり、工程能力の正確さ(つまりCpkにおける目標値からの偏移量(K)の検定)を見るには、一応十分な試料数と判断できる。
2)母分散の検定
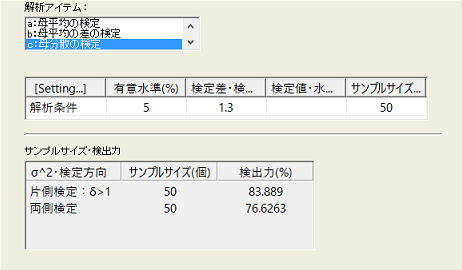
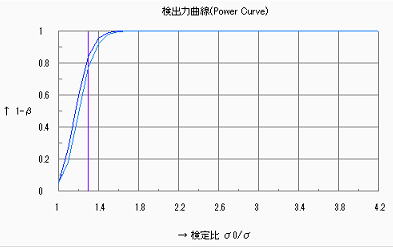
以下に示すように![]() =1.3において84%程度の検出力であり、工程能力の精度(つまりCp)を正確に見るには少し不足ではあるが、少な過ぎるというものではない。
=1.3において84%程度の検出力であり、工程能力の精度(つまりCp)を正確に見るには少し不足ではあるが、少な過ぎるというものではない。
6.纏め
サンプルサイズと検出力を求める際の検定差(比)は仮説検定を実施する際には表れない言葉であるが、要は評価者が知りたい情報の分解能だと思えば分かり易い。工程能力の「正確さ」であれば、そのずれ具合![]() を何σの分解能で判断したいかであり、0に漸近する程分解能は高くなり試料数は多くなる。工程能力の「精度」では、知りたい母標準偏差に対する相対比
を何σの分解能で判断したいかであり、0に漸近する程分解能は高くなり試料数は多くなる。工程能力の「精度」では、知りたい母標準偏差に対する相対比![]() が分解能となり、1に漸近する程分解能は高くなり試料数は多くなる。エンジニアはサンプルサイズを設計できないまでも、製作可能な試作品の個数が決まったら4.1項の表に示す該当試料数から、検定差(比)と検出力のバランスを見極めて欲しい。
が分解能となり、1に漸近する程分解能は高くなり試料数は多くなる。エンジニアはサンプルサイズを設計できないまでも、製作可能な試作品の個数が決まったら4.1項の表に示す該当試料数から、検定差(比)と検出力のバランスを見極めて欲しい。